 データの活用 |
９ 場合の数２ | 月 日（ ） |
| データの活用 |
９ 場合の数２ | 月 日（ ） |
| １ | 都立国分寺高校 （Ｒ７年） ★ | ５ | 九州国際大付属高校 （Ｒ６年） ★ |
| A,B,C,Dの生徒4人が左から順に横1列に並ぶとき,生徒Aと生徒Bが隣り合うようになる並び方は全部で何通りか。 |
6枚のカード から2枚を選んで一列に並べるとき,並べ方は何通りあるか答えなさい。 |
||
| ２ | 福岡大附属大濠高校 （Ｒ７年） ★★ | ６ | 中央大附属高校 （Ｒ７年） ★ |
| 4人を2つの組に分ける方法は[ ]通りある。ただし,誰もいない組は考えないものとする。 |
5人の生徒A,B,C,D,Eを横1列に並べる方法は何通りあるか求めなさい。ただし,ABCDEとEDCBAのように,逆に並べると同じになる並べ方は1通りと数えることとする。 |
||
| ３ | 青山学院高等部 （Ｒ５年） ★★★ | ７ | 慶応義塾志木高校 （Ｒ７年） ★★★ |
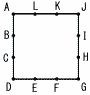 図のように,正方形の頂点と各辺を三等分する点の計12個の点A〜Lがある。これらの点から,次の条件で選んだ3点を結んでできる三角形の個数を求めよ。(1) 正方形の頂点を3つ含む。 (2) 正方形の頂点をちょうど2つ含む。 (3) 正方形の頂点を1つも含まない。 |
〇と書いてあるカードと,△と書いてあるカードが,それぞれたくさんある。これらのカードを,△と書いてあるカードが隣り合わないように横一列に並べていく。例えば3枚の力ードの並べ方は〇〇〇,〇〇△,〇△〇,△〇〇,△○△の5通りである。 (1) 4枚のカードの並へ方が何通りあるか求めよ。 (2) 5枚のカードの並べ方が何通りあるか求めよ。 (3) n枚のカードの並べ方がはじめて200通りを超えるときのnの値を求めよ。 |
||
| ４ | 明治学院東村山高校 （Ｒ６年） ★★ | ８ | 関西学院高等部 （Ｒ６年） ★★★ |
| 0から5までの数字が書かれたカードがそれぞれ1枚ずつあります。この中から3枚選んで3桁の整数を作るとき,次の場合が何通りあるか答えなさい。 (1) 百の位の数が偶数 (2) 3桁の整数が偶数 (3) 各位の数の和が偶数 |
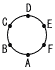 図のように,円周上に等間隔で6つの点A,B,C,D,E,Fが並んでいる。動点Pは最初点Ａの位置にあり,1個のサイコロを投げ,奇数の目が出れぱ時計回りに,偶数の目が出れぱ反時計回りに,出た目の数だけ円周上の点を移動する。サイコロを１回投げたとき,点Pが点Ａの位置にあるような目の出方は何通りあるか求めよ。 |
||
