 データの活用 |
８ 場合の数１ | 月 日（ ） |
| データの活用 |
８ 場合の数１ | 月 日（ ） |
| １ | 桐光学園高校 （Ｒ７年） ★★★ | ６ | 青山学院高等部 （Ｒ７年） ★★ |
 図のように,正方形ABCDの辺AB,BC,CD,DAの中点をそれぞれE,F,G,Hとする。これらの8個の点から3個を結んでできる二等辺三角形は何個あるか。 |
1個のさいころを繰り返し投げ,出てきた目の数の和を順に計算していく。次の場合の,順番も考えた目の出方は全部で何通りあるか。 (1) さいころを2回投げ終えたとき,和が9となる。 (2) さいころを3回投げ終えたとき,和が9となる。 (3) さいころを3回投げ終えたときに初めて和が9以上10以下となる。 |
||
| ２ | 東海大付属浦安高校 （Ｒ６年） ★★ | ||
| もも9個,梨3個をA,B,Cの3人に4個ずつ配ります。配り方は全部で[ ]通りになります。 |
|||
| ３ | 桃山学院高校 （Ｒ６年） ★★ | ７ | 関西学院高等部 （Ｒ７年） ★★★ |
| x＋y＋z＝9を満たす自然数x,y,zの組は何通りありますか｡ただしzはx以下の数とします。 |
大中小の3つのサイコロを同時に投げ,それぞれの出た目の数をx,y,zとするとき,\(\frac{x}2\)+\(\frac{y}3\)+\(\frac{z}4\)が整数になる目の出方は何通りあるか求めよ。 |
||
| ４ | ラ・サール高校 （Ｒ５年） ★★★ | ８ | 福知山成美高校 （Ｒ７年） ★ |
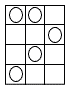 図のように,縦4マス,横3マスの長方形のマス目にいくつかの碁石を並べることを考える。縦に2つは続かない並べ方は何通りあるか。次の場合について答えよ。(1) 碁石を6個並べるとき (2) 碁石を5個並べるとき (3) 碁石を4個並べるとき |
 右の図のように同一円周上に6個の点が等間隔に並んでいる。(1) 6個の点から3個の点を選んで結び三角形を作ったとき,全部で何通り作れるか答えなさい。 (2) (1)の三角形のうち,直角三角形であるのは何通りか答えなさい。 |
||
| ５ | 早大高等学院 （Ｒ６年） ★ | ９ | 早稲田実業高等部 （Ｒ６年） ★★ |
| 大小2つのさいころを投げ,大きいさいころの目を十の位の数,小さいさいころの目を一の位の数とする,2けたの数mを作る。次の条件を満たすmは,それぞれ何個あるか求めよ。 (1) 3の倍数である。 (2) 素数である。 |
 の4枚のカードを  のように並べて式を作る。例えば, と並べるとその値は112である。式の値が3の倍数となるような並べ方は全部で何通りあるか。 |
||
