 図形 |
２６ 切断と切り口 | 月 日（ ） |
| 図形 |
２６ 切断と切り口 | 月 日（ ） |
| １ | 大阪教育大附属平野校舎高校 （Ｒ５年） ★ | ５ | お茶の水女子大附属高校 （Ｒ５年） ★★★ |
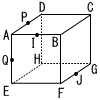 １辺の長さが4cmの立方体ABCD-EFGHがある。辺AB,FG,AD,AEの中点をそれぞれI,J,P,Qとする。次の3点を通る平面でこの立方体を切断するとき,切り口の形と切り口の周の長さを答えなさい。(1) P,Q,I (2) P,Q,F (3) P,Q,J |
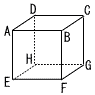 図のような１辺の長さが1の立方体ABCD-EFGHがある。4点A,F,G,Hを頂点とする三角すいSと,4点C,F,E,Hを頂点とする三角すいＴがあるとき,(1) 三角すいSの表面積を求めなさい。 (2) 辺AE上にAP:PE＝m:nとなるような点Pをとり,点Pを通り底面EFGHに平行な平面でこの2つの三角すいS,Tを切ったとき,2つの立体SとTの切り口の図形が重なった部分の面積をMとする。 ① m:n＝2:1のときのMの値を求めなさい。 ② m:n＝7:2のときのMの値を求めなさい。 |
||
| ２ | 埼玉県立高校 （Ｒ７年） ★★★ | ６ | 福岡大附属大濠高校 （Ｒ７年） ★★★ |
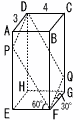 右の図のように,1辺の長さが6cmの正四面体 OABCの辺OB,OCの中点をそれぞれP,Qとします。 3点P,Q,Aを通る平面で正四面体OABCを切ったとき,頂点Bを含む立体の体積を求めなさい。 |
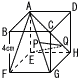 右の図のような１辺が4cmの立方体ABCD-EFGHから,四角すいA-EFGHをつくる。線分ACの中点をP,線分AH上に点Qをとる。点QがPQ＋QEを最小にするような点であるとき,線分PQの長さは[ ]cmである。 |
||
| ３ | 土浦日本大高校 （Ｒ６年） ★ | ７ | ラ・サール高校 （Ｒ６年） ★★★ |
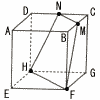 図は1辺の長さが2の立方体ABCD-EFGHである。辺BC,辺CDの中点をそれぞれM,Nとし,4点M,N,H,Fを通る平面でこの立方体を切り分けたとき,(1) MN＝[ ]であり,MF＝[ ]である． (2) 四角形MNHFの面積は[ ]である． (3) 切り分けた立体のうち,点Cを含む側の立体の体積は[ ]である。 |
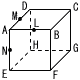 1辺の長さが2である立方体ABCD-EFGHにおいて,辺ABの中点をL,辺ADの中点をM,辺AEの中点をNとする。この立方体のすべての辺に接する球Oをとるとき,(1) 球Oの半径を求めよ． (2) 3点,L,M,Nを通る平面で球Oを切ったときの切り口の面積を求めよ。 (3) 3点L,M,Eを通る平面で球Oを切ったときの切り口の面積を求めよ。 |
||
| ４ | お茶の水女子大附属高校 （Ｒ７年） ★★★ | ８ | 京都市立柴野高校 （Ｒ７年） ★★★ |
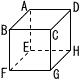 右の図のような1辺の長さが6cmの立方体がある。辺FG,辺GHの中点をそれぞれP,Qとする。(1) 点A,点P,点Qを通る平面でこの立方体を切ったときの切り口の図形名を答えなさい。 (2) (1)の切り口の図形の周の長さを求めなさい。 |
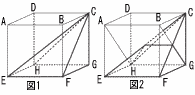 図のようにAB＝AD＝4cm,AE＝8cmの直方体ABCD-EFGHがある。辺GCの中点をＩ,辺FB上にあってFK＝2cmとなる点をK,辺HD上にあってHJ＝2cmとなる点をJとする。また,この直方体を3点.l,J,Kを通る平面で切断したときの切断面をSとする。(1) I Kの長さを求めなさい｡ (2) 切断面Sの面積を求めなさい｡ (3) この直方体が切断面Ｓによって2つの立体に分けられるとき,大きい方の立体の体積を求めなさい。 |
||
