 図形 |
２２ 直方体 | 月 日（ ） |
| 図形 |
２２ 直方体 | 月 日（ ） |
| １ | 岩手県立高校 （Ｒ５年） ★★★ | ４ | 広島県立高校 （Ｒ７年） ★ |
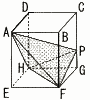 右の図は,AB＝6cm,AD＝5cm,AE＝7cmの直方体ABCD-EFGHです。(1) 線分AFの長さを求めなさい。 (2) 辺CG上にPG＝2cmとなるような点Pをとったとき,四面体AHFPの体積を求めなさい。 |
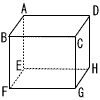 次の図のように,点A,B,C,D,E,F,G,Hを頂点とする直方体があり,AB＝4cm,AD＝6cm,AE＝3cmです。辺ADの中点を I,辺EFの中点をJとし,点Cと点I,点Iと点J, 点Jと点Cをそれぞれ結びます。このとき,△CIJの周の長さは何cmですか。 |
||
| ２ | 滝川第二高校 （Ｒ７年） ★★ | ５ | 京華高校 （Ｒ７年） ★★ |
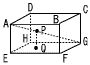 右の図のような,AB＝4cm,AD＝4cm,ＡE＝8cmの直方体ABCD-EFGHがあります。点Ｆから線分AGに垂線をひき,線分AGとの交点をPとします。(1) 線分AGの長さを求めなさい。 (2) 線分FPの長さを求めなさい。 (3) 立体P-EFGの体積を求めなさい。 |
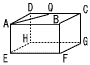 右の図のように直方体ABCD−EFGHがあり,線分EG と線FHの交点をPとする。点Qを辺AE上の点とし,線分 APと線分CQの交点をRとする。APとCQが垂直に交わるとき,(1) APの長さを求めよ。 (2) ARの長さを求めよ。 (3) 四角錐F−PRQEの体積を求めよ。 |
||
| ３ | 福岡県立高校 （Ｒ６年） ★★ | ６ | 西大和学園高校 （Ｒ６年） ★★★ |
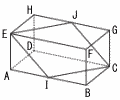 図は,AB＝8cm,BC＝4cm,AE＝4cmの直方体ABCDEFGHを表している。(1) 辺EF上に点P,辺FG上に点Qを,AP＋PQ＋QCの長さが最も短くなるようにとる。 このとき,線分PQの長さを求めよ。 (2) 辺ABの中点を I, 辺HGの中点をJとし,四角形EICJをつくったものである。 辺EF上に点Kを,EK＝KCとなるようにとるとき,四角すいKEICJの体積を求めよ。 |
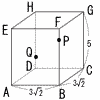 図のように,底面が一辺の長さ3√2の正方形で,高さが5の直方体がある。点P,Qはそれぞれ辺 BF,辺DH上の点で,FP＝1,DQ＝1である。このときPQの長さは[ア ]
である。三角形PACの面積は[イ ] であり,三角錐PACQの体積は[ウ ] である。 |
||
