| 21 立方体 | 月 日( ) |
| 21 立方体 | 月 日( ) |
| 1 | 東京電機大高校 (R5年) ★★ | 5 | 法政大第二高校 (R5年) ★★★ |
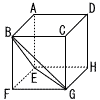 1辺の長さが12cmの立方体ABCD-EFGHがあります。 1辺の長さが12cmの立方体ABCD-EFGHがあります。(1) △BEGの面積を求めなさい。 (2) 線分BD上に,BP:PD=3:1となる点Pをとり,直線PFと△BEGとの交点をQとします。このとき,線分PQの長さを求めなさい。 |
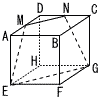 1辺の長さが8cmの立方体ABCD-EFGHがある。辺AD,CDの中点をそれぞれM,Nとする。 1辺の長さが8cmの立方体ABCD-EFGHがある。辺AD,CDの中点をそれぞれM,Nとする。(1) 四角形MEGNの面積を求めなさい。 (2) 点H四角形MEGNまでの距離を求めなさい。 |
||
| 2 | 早稲田佐賀高校 (R7年) ★★★ |
6 | 鎌倉学園高校 (R7年) ★★ |
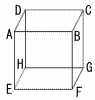 1辺の長さが3 1辺の長さが3 |
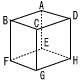 図のように,一辺の長さか6cmの立方体ABCD-EFGHがあります。辺AD,CDの中点をそれぞれM,Nとします。 図のように,一辺の長さか6cmの立方体ABCD-EFGHがあります。辺AD,CDの中点をそれぞれM,Nとします。(1) GNの長さを求めなさい。 (2) 立体DMN-HEGの体積を求めなさい。 (3) BHと四角形MNGEとの交点をPとするとき,BPの長さを求めなさい。 |
||
| 3 | 中央大附属高校 (R7年) ★★★ | ||
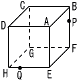 図のように,半径2の球が2つあり,それぞれが立方体の3つの面と接 し,2つの球が互いに外接している。立方体の1辺の長さを求めなさい。 図のように,半径2の球が2つあり,それぞれが立方体の3つの面と接 し,2つの球が互いに外接している。立方体の1辺の長さを求めなさい。 |
|||
| 4 | 市川高校 (R6年) ★★★ | 7 | 灘 高校 (R6年) ★★★ |
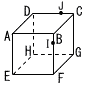 1辺の長さが8の立方体ABCD-EFGHについて,点I は辺BF上に点Jは辺CD上に存在し,BI:IF=CJ:JD=1:3である。 1辺の長さが8の立方体ABCD-EFGHについて,点I は辺BF上に点Jは辺CD上に存在し,BI:IF=CJ:JD=1:3である。(1) △IGHの面積を求めよ。 (2) Jから△IGHに下ろした垂線の足をKとするとき,KJの長さを求めよ。 (3) Kから正方形EFGHに下ろした垂線の足をLとするとき,KLの長さを求めよ。 |
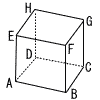 1辺の長さが1の立方体ABCD-EFGHがある。3点A,C,Fを通る平面と直線BHの交点を I とする。 1辺の長さが1の立方体ABCD-EFGHがある。3点A,C,Fを通る平面と直線BHの交点を I とする。(1) 線分BI の長さは[ ]である・ (2) 四面体ABCI の体積は[ ]である。 (3) 四面体ABCI の4つの面すべてに接する球の半径を rとするとき,(1/r)の値を求めよ。 |
||