| 20 半円 ・ 扇形 | 月 日( ) |
| 20 半円 ・ 扇形 | 月 日( ) |
| 1 | 西大和学園高校 (R5年) ★★ | 5 | 中央大附属横浜高校 (R5年) ★★ |
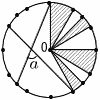 図は中心がOで半径が4の円周上に,円周を8等分する点と12等分する点を描いたものである。点が重複しているものもある。図の斜線部分の面積は(あ )である。また,図の角aの大きさは(い )°である。 図は中心がOで半径が4の円周上に,円周を8等分する点と12等分する点を描いたものである。点が重複しているものもある。図の斜線部分の面積は(あ )である。また,図の角aの大きさは(い )°である。 |
 図のように,ABを直径とする半径7の半円の内側に,CDを直径とする半径rの半円が内接している。ただし,直径CDは直径ABに対して30°傾いている。 図のように,ABを直径とする半径7の半円の内側に,CDを直径とする半径rの半円が内接している。ただし,直径CDは直径ABに対して30°傾いている。(1) 直径ABの中点と直径CDの中点の距離をdとするとき,r/dの値を求めなさい。 (2) rの値を求めなさい。 |
||
| 2 | 早稲田佐賀高校 (R7年) ★ | 6 | 桐光高校 (R6年) ★★★ |
 右の図は,中心角が90°,半径が9のおうぎ形OABであり,点C,Dは弧ABを3等分した点である。また,OA 右の図は,中心角が90°,半径が9のおうぎ形OABであり,点C,Dは弧ABを3等分した点である。また,OA |
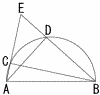
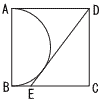 図のように,正方形ABCDの辺ABを直径とする半円と,頂点Dと辺BC上の点Eを結んだ線分が接している。線分DEの長さが6cmのとき,半円の面積を求めよ。 図のように,正方形ABCDの辺ABを直径とする半円と,頂点Dと辺BC上の点Eを結んだ線分が接している。線分DEの長さが6cmのとき,半円の面積を求めよ。 |
||
| 3 | 青山学院高等部 (R6年) ★★★ | 7 | 追手門学院大手前高校 (R7年) ★★ |
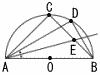 ABを直径とする半円Oがあり,弧AB上に ABを直径とする半円Oがあり,弧AB上に(1) 線分AEの長さを求めよ. (2) 線分BEの長さを求めよ. (3) 線分CDの長さを求めよ. |
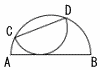
 右の図のように,線分ABを直径とする半円がある。弧AB上に2点C,Dがあり,直線ACと直線BDの交点をEとする。AC=2,CE=6,DE=4のとき, 右の図のように,線分ABを直径とする半円がある。弧AB上に2点C,Dがあり,直線ACと直線BDの交点をEとする。AC=2,CE=6,DE=4のとき,(1) △ADE∽△BCEを証明しなさい。 (2) 線分BDの長さを求めなさい。 (3) △BCEの面積を求めなさい。 |
||
| 4 | 大阪星光学院高校 (R7年) ★★ | 8 | 東京学芸大附属高校 (R7年) ★★ |
 右の図のようにAB,,CBをそれぞれ直径とする大小2つの半円があり,AEは小さい方の半円上の点 Dにおける接線である。 右の図のようにAB,,CBをそれぞれ直径とする大小2つの半円があり,AEは小さい方の半円上の点 Dにおける接線である。 |
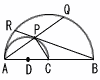
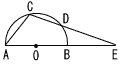 図のように,中心角が120°のおうぎ形OABがあり,2点C,DはAB上にある。AC= 3πcm,CD=4πcm,DB=5πcmである。線分ADと線分BCの交点を Eとするとき,∠AEBの大きさ を求めなさい。 図のように,中心角が120°のおうぎ形OABがあり,2点C,DはAB上にある。AC= 3πcm,CD=4πcm,DB=5πcmである。線分ADと線分BCの交点を Eとするとき,∠AEBの大きさ を求めなさい。 |
||