| 20 半円 ・ 扇形 (略解) | ||
| 20 半円 ・ 扇形 (略解) | ||
| 1 | 西大和学園高校 (R5年) ★★ | 5 | 中央大附属横浜高校 (R5年) ★★ | |||
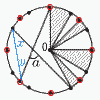 図は中心がOで半径が4の円周上に,円周を8等分する点と12等分する点を描いたものである。点が重複しているものもある。図の斜線部分の面積は(あ )である。また,図の角aの大きさは(い )°である。 図は中心がOで半径が4の円周上に,円周を8等分する点と12等分する点を描いたものである。点が重複しているものもある。図の斜線部分の面積は(あ )である。また,図の角aの大きさは(い )°である。【解】 8等分点(45°の扇形), 12等分点(30°の扇形) 斜線部分(扇形の合計)は90° あ=42π×=4π ∠xは円周の5/24で,∠x=360×(5/24)÷2=75/2 ∠yは円周の い=∠a=(75/2)+30=135/2 (67.5) |
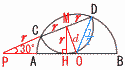 図のように,ABを直径とする半径7の半円の内側に,CDを直径とする半径rの半円が内接している。 図のように,ABを直径とする半径7の半円の内側に,CDを直径とする半径rの半円が内接している。(1) 直径ABの中点と直径CDの中点の距離をdとするとき,r/dの値を求めなさい。 【解】PH=√3r △MPH∽△OPMより,r:d=√3r:2rで,r/d= (2) rの値を求めなさい。 【解】△ODMで r2+d2=r2+( |
|||||
| 2 | 早稲田佐賀高校 (R7年) ★ | 6 |
桐光高校 (R6年) ★★★ | |||
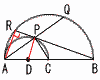 右の図は,中心角が90°,半径が9のおうぎ形OABであり,点C,Dは弧ABを3等分した点である。また,OA 右の図は,中心角が90°,半径が9のおうぎ形OABであり,点C,Dは弧ABを3等分した点である。また,OA【解】斜線=△ODF+ ところが,△ODF=△OCE(斜辺と1鋭角相等)だから, 斜線= |
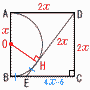 図のように,正方形ABCDの辺ABを直径とする半円と,頂点Dと辺BC上の点Eを結んだ線分が接している。線分DEの長さが6cmのとき,半円の面積を求めよ。 図のように,正方形ABCDの辺ABを直径とする半円と,頂点Dと辺BC上の点Eを結んだ線分が接している。線分DEの長さが6cmのとき,半円の面積を求めよ。【解】半円の半径をxとすると,DA=DH=DC=2x EB=EH=6−2xより,EC=BC−BE=2x−(6−2x)=4x−6 △DECで,(2x)2+(4x−6)2=62 4x(5x−12)=0で,x= 半円=( |
|||||
| 3 | 青山学院高等部 (R6年) ★★★ | 7 | 追手門学院大手前高校 (R7年) ★★ | |||
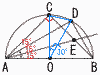 AB=6cm,BD=3cmのとき, AB=6cm,BD=3cmのとき,(1) 線分AEの長さを求めよ. 【解】△ACEで,AC=3√2,∠AEC=60° AE= (2) 線分BEの長さを求めよ. 【解】BE=CB−CE=3√2− 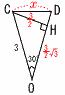 (3) 線分CDの長さを求めよ. (3) 線分CDの長さを求めよ.【解】△OCDは頂角30°の二等辺三角形 △CDHで,x2=( x2= x=CD= |
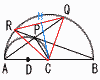 右の図のように,線分ABを直径とする半円がある。弧AB上に2点C,Dがあり,直線ACと直線BDの交点をEとする。AC=2,CE=6,DE=4のとき, 右の図のように,線分ABを直径とする半円がある。弧AB上に2点C,Dがあり,直線ACと直線BDの交点をEとする。AC=2,CE=6,DE=4のとき,(1) △ADE∽△BCEを証明しなさい。 【証明】△ADE∽△BCEで,
(2) 線分BDの長さを求めなさい。 【解】(1)より,4:6=8:BEで,BE=12 よって,BD=12−4=8 (3) △BCEの面積を求めなさい。 【解】△BCE(∠E=60°)= |
|||||
| 4 | 大阪星光学院高校 (R7年) ★★ | 8 | 東京学芸大附属高校 (R7年) ★★ | |||
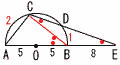 右の図のようにAB,,CBをそれぞれ直径とする大小2つの半円があり,AEは小さい方の半円上の点 Dにおける接線である。 右の図のようにAB,,CBをそれぞれ直径とする大小2つの半円があり,AEは小さい方の半円上の点 Dにおける接線である。【解】 |
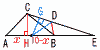 図のように,中心角が120°のおうぎ形OABがあり,2点C,DはAB上にある。AC= 3πcm,CD=4πcm,DB=5πcmである。線分ADと線分BCの交点を Eとするとき,∠AEBの大きさ を求めなさい。 図のように,中心角が120°のおうぎ形OABがあり,2点C,DはAB上にある。AC= 3πcm,CD=4πcm,DB=5πcmである。線分ADと線分BCの交点を Eとするとき,∠AEBの大きさ を求めなさい。【解】 同様に, 四OAEBで, ∠AEB=360−(120+55+45)=140° |
|||||