| 17 多角形 | 月 日( ) |
| 17 多角形 | 月 日( ) |
| 1 | 福岡大附属大濠高校 (R7年) ★ | 6 | 鳥取県立高校 (R7年) ★★★ |
 右の図のように,正六角形ABCDEFがあり,点P,Qはそれぞれ辺AB,EFの中点である。四角形APQFと四角形PBEQの面積の比は[ ]である。 右の図のように,正六角形ABCDEFがあり,点P,Qはそれぞれ辺AB,EFの中点である。四角形APQFと四角形PBEQの面積の比は[ ]である。 |
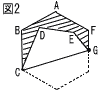
 次の図は,正七角形をもとにして作られた「ルーロ−の七角形」(頂点Aを中心に,対角線ADの長さを半径とする弧DEをかき,他の頂点についても同様に作図する)である。さしわたし幅(2本の平行線の間隔)がhcmであるとき,この「ルーローの七角形」の周の長さを求めなさい。 次の図は,正七角形をもとにして作られた「ルーロ−の七角形」(頂点Aを中心に,対角線ADの長さを半径とする弧DEをかき,他の頂点についても同様に作図する)である。さしわたし幅(2本の平行線の間隔)がhcmであるとき,この「ルーローの七角形」の周の長さを求めなさい。 |
||
| 2 | 市立西京高校 (R5年) ★ | 7 | 福岡県立高校 (R7年) ★★★ |
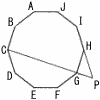 正十角形ABCDEFGHIJ において,直線CGと直線HI の交点をPとする。∠CPI の大きさを求めよ。 正十角形ABCDEFGHIJ において,直線CGと直線HI の交点をPとする。∠CPI の大きさを求めよ。 |
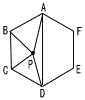
 円Oの円周上に5点A,B,C,D,Eをとり,五角形ABCDEをつくる。 円Oの円周上に5点A,B,C,D,Eをとり,五角形ABCDEをつくる。図1は,五角形ABCDEにおいて,点Bと点Eを結ぴ,BE (1) 図2は,図1において,五角形ABCDEが,正五角形となる場合を表しており,点Aと点Cを結び,線分ACと線分BEとの交点をGとしたものである。 このとき,∠AGEの大きさを求めなさい。 (2) 図3は,図1において,点Aと点C,点Aと点D,点Cと点Eを結ぴ, 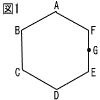 線分BEと線分AC,線分ADとの交点をそれぞれP,Qとし,線分ADと線分CEとの交点をRとしたものである。 線分BEと線分AC,線分ADとの交点をそれぞれP,Qとし,線分ADと線分CEとの交点をRとしたものである。図3において,△ABP∽△ADEであることを証明しなさい。 (3) 図4は,図3において∠EAD=30°, AP:PC=3:2,線分ACが円0の直径となる場合を表している。 図4において,AE=6cmのとき,円Oの直径を求めなさい。 |
||
| 3 | 國學院久我山高校 (R5年) ★★ | ||
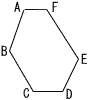 図のような,6つの内角の大きさがすべて等しく,周の長さが39の六角形ABCDEFがある。AB=8,BC=7,CD=6のとき,EF=( )となる。 図のような,6つの内角の大きさがすべて等しく,周の長さが39の六角形ABCDEFがある。AB=8,BC=7,CD=6のとき,EF=( )となる。 |
|||
| 4 | 西大和学園高校 (R7年) ★★ | ||
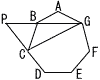 図の七角形ABCDEFGは正七角形である。直線BGと直線CDの交点をPとするとき,∠AGC=∠GPCであることを証明せよ。 図の七角形ABCDEFGは正七角形である。直線BGと直線CDの交点をPとするとき,∠AGC=∠GPCであることを証明せよ。 |
|||
| 5 | 桐蔭学園高校 (R6年) ★ | 8 | 駿台甲府高校 (R6年) ★ |
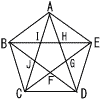
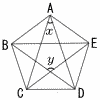 図のように,正五角形ABCDEがある。このとき,∠xの大きさは[ ]°,∠yの大きさは[ ]°である。 図のように,正五角形ABCDEがある。このとき,∠xの大きさは[ ]°,∠yの大きさは[ ]°である。 |
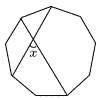 右の図の正九角形において,∠xの大きさを求めよ。 右の図の正九角形において,∠xの大きさを求めよ。 |
||