 図形 |
１６ 正方形 | 月 日（ ） |
| 図形 |
１６ 正方形 | 月 日（ ） |
| １ | 都立墨田川高校 （Ｒ５年） ★ | ５ | 愛知県立高校 （Ｒ６年） ★★★ |
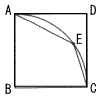 右の図において,四角形ABCDは正方形,弧ACは,頂点Bを中心とし,線分BAを半径とする円の周の一部である。弧AC上にあり,頂点A,頂点Cのいずれにも一致しない点をEとし,頂点Aと点E,頂点Cと点Eをそれぞれ結ぶ。 このとき,∠EAD＋∠ECDの大きさは何度か。 ただし,∠EADと∠ECDは,ともに四角形AECDの内角とする。 |
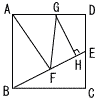 図で,四角形ABCDは正方形,Eは辺DCの中点,Fは線分EBの中点,Gは辺AD上の点で,∠GAF＝∠GFEである。また,Hは線分EB上の点で,∠GHE=
90°である。AB＝4cmのとき,(1) 線分EFの長さは[ ]cmである。 (2) 線分HFの長さは線分EBの長さの[ ]倍である。 |
||
| ２ | ラ・サール高校 （Ｒ５年） ★★★ | ６ | 岡山県立高校 （Ｒ７年） ★★★ |
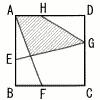 図のように,1辺の長さが3の正方形ABCDの各辺にBE＝BF＝DG＝AH＝1となる点E,F,G,Hをとる。2直線AFとEGの交点をPとするとき,(1) 長さの比 EP:PG (2) 四角形APGHの面積 |
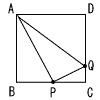 図のように,1辺の長さが4cmの正方形ABCDがあり,辺BCの中点をEとし,線分AEを1辺とする正方形 AEFGをかきます。点Aと点C,点Aと点F,点Cと点Fをそれぞれ結び,線分EFと線分ACの交点をHとします。(1) 線分AEの長さを求めなさい。 (2) △AHF∽△EHCを証明しなさい。 (3) ∠ACFの大きさを求めなさい。 (4) 線分CHの長さを求めなさい。 (5) 3点A,E,Fを通る円の中心をP,3点C,F,Hを通る円の中心をQとします。このとき,線分PQの長さを求めなさい。 |
||
| ３ | 立教新座高校 （Ｒ７年） ★★★ | ||
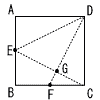 図のような,1辺の長さが4cmの正方形 ABCDと辺BCを半径とする円Cの一部があり ます。辺AD上を動く点をEとし,線分CEとBDの交点をPとします。また,点Pを接点とする円Cの接線を引き,辺AB.,ADとの交点をそれぞれQ.,Rとします。(1) ∠PCD=40°のとき,∠AQPの大きさを求めなさい。 (2) CE＝2  cmのとき,AEの長さを求めなさい。(3) AE＝1cmのとき,△AQRの面積を求めなさい。 (4) PB＝PCのとき,四角形AQPEの面積を求めなさい。 |
|||
| ４ | 京都市立西京高校 （Ｒ７年） ★★★ | ７ | 立命館高校 （Ｒ６年） ★★ |
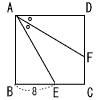 1辺の長さが3cmの正方形ABCDにおいて,辺CD上にDEの長さが1cmとなるように点Eを とる。線分AEと線分BDの交点をFとするとき,△FBEの面積を求めよ。 |
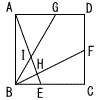 右の図の四角形ABCDは１辺の長さが10cmの正方形です。辺BC上にBE:EB＝1:2となる点E,辺CD上にCF:FD＝1:1となる点F,辺AD上にAG:GD＝3:2となる点Gをとります。線分AEと線分BF,BGとの交点をそれぞれH,I
とするとき,△BHI の面積を求めなさい。 |
||
