| 15 長方形 | 月 日( ) |
| 15 長方形 | 月 日( ) |
| 1 | 常盤高校 (R7年) ★ | 5 | 立命館守山高校 (R7年) ★★ |
 図の長方形で,斜線部分の面積を最も簡単な式で表すと[ ]である。 図の長方形で,斜線部分の面積を最も簡単な式で表すと[ ]である。 |
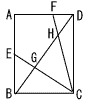
 右の図で,四角形 ABCDはAB=6cm,BC=8cmの長方形である。辺CD上にCE:ED=2:1となる点Eをとり,辺 BCの中点をFとする。また,線分BEと線分ACとの交点をGとし,点Fと点Gを結ぶ。このとき,△CGF
の面積を求めなさい。 右の図で,四角形 ABCDはAB=6cm,BC=8cmの長方形である。辺CD上にCE:ED=2:1となる点Eをとり,辺 BCの中点をFとする。また,線分BEと線分ACとの交点をGとし,点Fと点Gを結ぶ。このとき,△CGF
の面積を求めなさい。 |
||
| 2 | 広島大附属高校 (R5年) ★★ | 6 | 大阪産大附属高校 (R7年) ★★ |
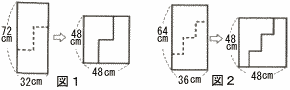 長方形には,図1,図2のように…の線で2つに分割して並べ替えることで,正方形にすることができるものがあります。図1のような切り方を「2段切り」,図2のような切り方を「3段切り」とよぶことにします。 長方形には,図1,図2のように…の線で2つに分割して並べ替えることで,正方形にすることができるものがあります。図1のような切り方を「2段切り」,図2のような切り方を「3段切り」とよぶことにします。縦の長さが128cm,横の長さがxcmの長方形を「7段切り」して正方形にできるとき,xの値を求めなさい。 |
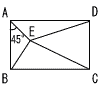 右の図のように,長方形ABCDがあります。点Eは長方形ABCDの内部の点で∠BAE=45°です。また点Eを通り辺ABに平行な直線をひき,辺AD,辺BCとの交点をそれぞれF,Gとします。 右の図のように,長方形ABCDがあります。点Eは長方形ABCDの内部の点で∠BAE=45°です。また点Eを通り辺ABに平行な直線をひき,辺AD,辺BCとの交点をそれぞれF,Gとします。長方形ABCD,△ABE,△AEDの面積がそれぞれ40cm2,5cm2,8cm2のとき, (1) 長方形ABGFの面積を求めなさい。 (2) △DECの面積を求めなさい。 (3) 1辺ABの長さを求めなさい。 (4) 辺EGの長さを求めなさい。 |
||
| 3 | 法政大高校 (R6年) ★★ | ||
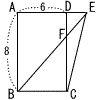 右の図のような長方形ABCDがあり,ADの延長線上に点Eをとり,BEとCDとの交点をFとする。△CEFの面積が8のとき,DEの長さを求めなさい。 右の図のような長方形ABCDがあり,ADの延長線上に点Eをとり,BEとCDとの交点をFとする。△CEFの面積が8のとき,DEの長さを求めなさい。 |
|||
| 4 | 香川県立高校 (R6年) ★★ | 7 | 愛知県立高校 (R7年) ★★★ |
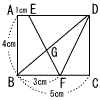 右の図のような,長方形ABCDがある。辺AD上に2点A,Dと異なる点Eをとり,辺BC上に2点B,Cと異なる点Fをとる。線分EFと対角線BDとの交点をGとする。また,点Dと点Fを結ぶ。 右の図のような,長方形ABCDがある。辺AD上に2点A,Dと異なる点Eをとり,辺BC上に2点B,Cと異なる点Fをとる。線分EFと対角線BDとの交点をGとする。また,点Dと点Fを結ぶ。AB=4cm,BC=5cm,AE=1cm,BF=3cmであるとき, 1) 線分DFの長さは何cmか。 (2) 四角形ABGEの面積は何cm2か。 |
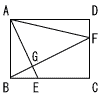
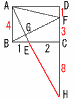 図で,四角形ABCDは長方形,Eは辺AD上の点で,AE:ED=2:1,Fは辺DC上の点で,DBLEFである。 また,Gは線分DBとEFの交点である。AB=4cm,AD=6cmのとき, 図で,四角形ABCDは長方形,Eは辺AD上の点で,AE:ED=2:1,Fは辺DC上の点で,DBLEFである。 また,Gは線分DBとEFの交点である。AB=4cm,AD=6cmのとき,(1) 線分DGの長さは線分DBの長さの[ ]倍である。 (2) △GBFの面積は[ ]cm² である。 |
||