| 丂侾俁丂捈妏嶰妏宍 | 丂丂丂寧丂丂丂擔乮丂丂乯 |
| 丂侾俁丂捈妏嶰妏宍 | 丂丂丂寧丂丂丂擔乮丂丂乯 |
| 侾 | 帬夑導棫崅峑丂乮俼俆擭乯丂仛 | 係 | 崄愳導棫崅峑丂乮俼俈擭乯丂仛 |
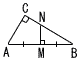 丂佢C=90亱偺捈妏嶰妏宍ABC偱,曈AB,CA偺挿偝傪偦傟偧傟10,5偲偟傑偡丅 丂佢C=90亱偺捈妏嶰妏宍ABC偱,曈AB,CA偺挿偝傪偦傟偧傟10,5偲偟傑偡丅(1) 恾偺傛偆偵,曈AB偺悅捈擇摍暘慄傪傂偒,曈AB,BC偲偺岎揰傪偦傟偧傟M,N偲偟傑偡丅偙偺偲偒,仮ABC偲仮NBM偺柺愊斾傪媮傔側偝偄丅 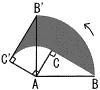 (2) 恾偺傛偆偵,捈妏嶰妏宍ABC傪捀揰A傪拞怱偵90亱夞揮偝偣傑偡丅偙偺偲偒,曈BC偑捠夁偟偨偲偒偵偱偒傞幬慄晹偺柺愊傪媮傔側偝偄丅 丂 |
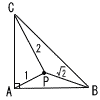 丂塃偺恾偺傛偆側,佢ACB亖90亱偺捈妏嶰妏宍ABC偑偁傝,AB亖10cm,BC亖6cm偱偁傞丅揰D偼曈AB忋偺揰偱,BD亖3cm偱偁傞丅揰E偼曈AC忋偺揰偱,CE亖3cm偱偁傞丅揰D偲揰俤傪寢傇丅 丂塃偺恾偺傛偆側,佢ACB亖90亱偺捈妏嶰妏宍ABC偑偁傝,AB亖10cm,BC亖6cm偱偁傞丅揰D偼曈AB忋偺揰偱,BD亖3cm偱偁傞丅揰E偼曈AC忋偺揰偱,CE亖3cm偱偁傞丅揰D偲揰俤傪寢傇丅丂慄暘AD忋偵揰F傪,巐妏宍BCED偺柺愊偲仮BCF偺柺愊偑摍偟偔側傞傛偆偵偲傞偲偒,慄暘DF偺挿偝偼壗cm偐丅 丂 |
||
| 俀 | 愮梩導棫崅峑丂乮俼俆擭乯丂仛仛仛 | 俇 | 憗戝杮彲崅峑丂乮俼係擭乯丂仛仛仛 |
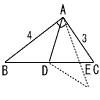
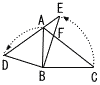 丂塃偺恾偺仮ABC偼,AB亖3cm,BC亖4cm,佢ABC亖90亱偺捈妏嶰妏宍偱偁傞丅仮DBE偼,仮ABC傪,揰B傪拞怱偲偟偰,栴報偺曽岦偵夞揮偝偣偨傕偺偱偁傝,仮DBE偺曈DE忋偵仮ABC偺捀揰A偑偁傞丅傑偨,曈CA偲曈BE偺岎揰傪F偲偡傞丅 丂塃偺恾偺仮ABC偼,AB亖3cm,BC亖4cm,佢ABC亖90亱偺捈妏嶰妏宍偱偁傞丅仮DBE偼,仮ABC傪,揰B傪拞怱偲偟偰,栴報偺曽岦偵夞揮偝偣偨傕偺偱偁傝,仮DBE偺曈DE忋偵仮ABC偺捀揰A偑偁傞丅傑偨,曈CA偲曈BE偺岎揰傪F偲偡傞丅(1) 慄暘AE偺挿偝傪媮傔側偝偄丅 (2) 仮ABF偺柺愊傪媮傔側偝偄丅 丂 |
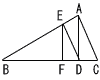 丂嶰妏宍ABC偵偍偄偰,佢BAC亖90亱,AB亖4,BC亖5,CA亖3偱偁傞丅揰E偼曈AB忋偵,揰D,F偼曈BC忋偵偁傞丅佢ADC亖佢DEA亖佢EFD=
90亱偱偁傞偲偒,慄暘EF偺挿偝傪媮傔傛丅 丂嶰妏宍ABC偵偍偄偰,佢BAC亖90亱,AB亖4,BC亖5,CA亖3偱偁傞丅揰E偼曈AB忋偵,揰D,F偼曈BC忋偵偁傞丅佢ADC亖佢DEA亖佢EFD=
90亱偱偁傞偲偒,慄暘EF偺挿偝傪媮傔傛丅丂 |
||
| 俁 | 擔杮戝戞嶰崅峑丂乮俼俇擭乯丂仛仛仛 | 俇 | 敓娰儔丒僒乕儖崅峑丂乮俼俈擭乯丂仛仛仛 |
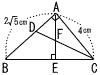 丂塃偺恾偺傛偆偵,AB亖2併5cm,AC亖4cm,佢A亖90亱偺仮ABC偑偁傞丅佢C偺擇摍暘慄偲曈AB偲偺岎揰傪D,傑偨,捀揰俙偐傜曈BC偵悅慄AE傪堷偒,CD偲偺岎揰傪F偲偡傞丅 丂塃偺恾偺傛偆偵,AB亖2併5cm,AC亖4cm,佢A亖90亱偺仮ABC偑偁傞丅佢C偺擇摍暘慄偲曈AB偲偺岎揰傪D,傑偨,捀揰俙偐傜曈BC偵悅慄AE傪堷偒,CD偲偺岎揰傪F偲偡傞丅(1) AD:DB偺挿偝偺斾傪,傕偭偲傕娙扨,側惍悢偺斾偱摎偊側偝偄丅 (2) EC偺挿偝傪媮傔側偝偄丅 (3) 仮ADF:仮ECF偺柺愊偺斾傪,傕偭偲傕娙扨側惍悢偺斾偱摎偊側偝偄丅 丂 |
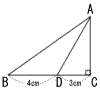 丂恾偺傛偆偵佢ACB亖90亱偺捈妏嶰妏宍偑偁傝丄曈BC忋偵BD亖4噋,DC亖3噋偲側傞傛偆偵揰D傪偲傞丅佢BAD亖佢CAD偺偲偒,AC偺挿偝傪媮傔側偝偄丅 丂恾偺傛偆偵佢ACB亖90亱偺捈妏嶰妏宍偑偁傝丄曈BC忋偵BD亖4噋,DC亖3噋偲側傞傛偆偵揰D傪偲傞丅佢BAD亖佢CAD偺偲偒,AC偺挿偝傪媮傔側偝偄丅 丂 |
||
| 俈 | 拞墰戝悪暲崅峑丂乮俼俈擭乯丂仛仛 | ||
 丂恾偺傛偆偵,1曈偺挿偝偑t偺惓嶰妏宍偲,1曈偺挿偝偑s偺惓曽宍偲,墌偑屳偄偵愙偟偰偄傑偡丅惓嶰妏宍,惓曽宍,墌偑偄偢傟傕奜懁偺捈妏嶰妏宍ABC偵傕愙偟偰偄傞偲偒,(偨偩偟,佢B = 90亱) 丂恾偺傛偆偵,1曈偺挿偝偑t偺惓嶰妏宍偲,1曈偺挿偝偑s偺惓曽宍偲,墌偑屳偄偵愙偟偰偄傑偡丅惓嶰妏宍,惓曽宍,墌偑偄偢傟傕奜懁偺捈妏嶰妏宍ABC偵傕愙偟偰偄傞偲偒,(偨偩偟,佢B = 90亱)(1) 佢ACB偺戝偒偝傪媮傔側偝偄丅 (2) 惓嶰妏宍偺1曈偺挿偝t偼,惓曽宍偺1曈偺挿偝s偺壗攞偵側傞偐摎偊側偝偄丅 丂 |
|||