| �P�R�@���p�O�p�`�@�i�����j | ||
| �P�R�@���p�O�p�`�@�i�����j | ||
| �P | ���ꌧ�����Z�@�i�q�T�N�j�@�� | �S | ���쌧�����Z�@�i�q�V�N�j�@�� | |||||||||||||||
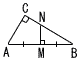 �@��C=90���̒��p�O�p�`ABC��,��AB,CA�̒�����10,5�Ƃ��܂��B �@��C=90���̒��p�O�p�`ABC��,��AB,CA�̒�����10,5�Ƃ��܂��B(1) ��ABC�Ɓ�NBM�̖ʐϔ�����߂Ȃ����B �y���zBC��5��3 ��ABC�䁢NBM(���3:1) 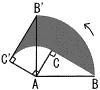 �@�ʐϔ䁁(��3)2:12��3:1 �@�ʐϔ䁁(��3)2:12��3:1(2) ��BC���ʉ߂����Ƃ��ɂł���ΐ����̖ʐς����߂Ȃ����B �y���z(��AB'C'�{��`ABB')�|(��`ACC'�{��ABC) �@����`ABB'�|��`ACC'��102���~ �@��25���| |
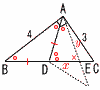 �@�E�̐}�̂悤��,��ACB��90���̒��p�O�p�`ABC������,AB��10cm,BC��6cm�ł���B�_D�͕�AB��̓_��,BD��3cm�ł���B�_E�͕�AC��̓_��,CE��3cm�ł���B�_D�Ɠ_�d�����ԁB �@�E�̐}�̂悤��,��ACB��90���̒��p�O�p�`ABC������,AB��10cm,BC��6cm�ł���B�_D�͕�AB��̓_��,BD��3cm�ł���B�_E�͕�AC��̓_��,CE��3cm�ł���B�_D�Ɠ_�d�����ԁB�@����AD��ɓ_F��,�l�p�`BCED�̖ʐςƁ�BCF�̖ʐς��������Ȃ�悤�ɂƂ�Ƃ�,����DF�̒����͉�cm���B �y���zE����CD�̕��s�������� ��ABC��,AC��8 ��ADE��,AD:DF��AC:CE���,7:DF��8:3��,DF��21/8cm |
|||||||||||||||||
| �Q | ��t�������Z�@�i�q�T�N�j�@������ | �T | ����{�����Z�@�i�q�S�N�j�@������ | |||||||||||||||
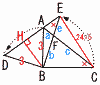 (1) ����AE�̒��������߂Ȃ����B (1) ����AE�̒��������߂Ȃ����B�y���z��DBE����ABC��12cm2 BH�� AE��DE�|DA��5�| (2) ��ABF�̖ʐς����߂Ȃ����B �y���z��AFE�䁢BFC���,��:����7:20�c�A ��ACE��,CE��24/5 �@��ABF�䁢ECF���,b:c��5:8�c�C �A�C���,a:c��(7/20)��:(8/5)b��7:32 ��ABF����ABC�~(7/39)��6�~(7/39)��14/13cm2 |
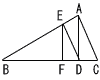 �@��ADC����DEA����EFD= 90���ł���Ƃ�,����EF�̒��������߂�B �@��ADC����DEA����EFD= 90���ł���Ƃ�,����EF�̒��������߂�B�y���z�i�E�}�Q�Ɓj ��ABC�䁢DAC���, �@AD��AB�~ 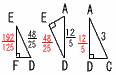 ��ABC�䁢EDA���, ��ABC�䁢EDA���,�@DE��AB�~( ��ABC�䁢FED���,
|
|||||||||||||||||
| �R | ���{���O���Z�@�i�q�U�N�j�@���� | �U | ���ك��E�T�[�����Z�@�i�q�V�N�j�@�� | |||||||||||||||
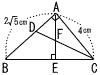 �@�E�̐}�̂悤��,AB��2��5cm,AC��4cm,��A��90���́�ABC������B��C�̓����ƕ�AB�Ƃ̌�_��D,�܂�,���_�`�����BC�ɐ���AE������,CD�Ƃ̌�_��F�Ƃ���B �@�E�̐}�̂悤��,AB��2��5cm,AC��4cm,��A��90���́�ABC������B��C�̓����ƕ�AB�Ƃ̌�_��D,�܂�,���_�`�����BC�ɐ���AE������,CD�Ƃ̌�_��F�Ƃ���B(1) AD:DB�̒����̔��,�����Ƃ��ȒP,�Ȑ����̔�œ����Ȃ����B �y���z BC����(2��52)�{42��6 CD�͓���������,AD:DB��4:6��2:3 (2) EC�̒��������߂Ȃ����B �y���z ��ABC�䁢EAC(������6:4��3:2) EC��AC�~ (3) ��ADF:��ECF�̖ʐς̔��,�����Ƃ��ȒP�Ȑ����̔�œ����Ȃ����B �y���z ��ADC�䁢EFC�i������4: �@DC:FC��3:2���,DF:FC��1:2��,��ADF:��AFC��1:2�c�A ��AEC��,AF:FE��4: �A�C���,��ADF:��ECF��3:4�@ �@�@�@�@�@�@�@�@�@�@�@ |
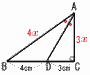 �@�}�̂悤�Ɂ�ACB��90���̒��p�O�p�`������A��BC���BD��4�p,DC��3�p�ƂȂ�悤�ɓ_D���Ƃ�B��BAD����CAD�̂Ƃ�,AC�̒��������߂Ȃ����B �@�}�̂悤�Ɂ�ACB��90���̒��p�O�p�`������A��BC���BD��4�p,DC��3�p�ƂȂ�悤�ɓ_D���Ƃ�B��BAD����CAD�̂Ƃ�,AC�̒��������߂Ȃ����B �y���zAB:AC��4:3���,AB��4x,AC��3x�Ƃ����, ��ABC�ŁC(3x)2�{72��(4x)2���,x�� �@�����,AC��3x��3 |
|||||||||||||||||
| �V | �����吙�����Z�@�i�q�V�N�j�@���� | |||||||||||||||||
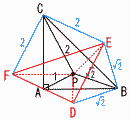 �@�}�̂悤��,1�ӂ̒�����t�̐��O�p�`��,1�ӂ̒�����s�̐����`��,�~���݂��ɐڂ��Ă��܂��B���O�p�`,�����`,�~����������O���̒��p�O�p�`ABC�ɂ��ڂ��Ă���Ƃ�,(������,��B = 90��) �@�}�̂悤��,1�ӂ̒�����t�̐��O�p�`��,1�ӂ̒�����s�̐����`��,�~���݂��ɐڂ��Ă��܂��B���O�p�`,�����`,�~����������O���̒��p�O�p�`ABC�ɂ��ڂ��Ă���Ƃ�,(������,��B = 90��)(1) ��ACB�̑傫�������߂Ȃ����B �y���z��DEC��,��E��60��������,��ACB��30�� (2) ���O�p�`��1�ӂ̒���t��,�����`��1�ӂ̒���s�̉��{�ɂȂ邩�����Ȃ����B �y���z����FI �����낷��,�Z��60��
�@t��s�� (3�{ |
||||||||||||||||||