 図形 |
１２ 二等辺三角形 | 月 日（ ） |
| 図形 |
１２ 二等辺三角形 | 月 日（ ） |
| １ | 盈進学園高校 （Ｒ５年） ★★ | ５ | 灘 高校 （Ｒ５年） ★★ |
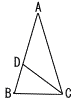 次のようなAB＝AC,BC＝AD＝CD,BC＝1cmの図形があります。(1) ∠ADCの大きさを求めなさい。 (2) BDの長さを求めなさい。 (3) ACの長さを求めなさい。 |
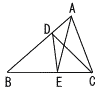 右の図において,BD＝DC＝CA,BE＝EAである。∠DEAの大きさが32度のとき,∠ABCの大きさは( )度である。 |
||
| ２ | 千葉県立高校 （Ｒ７年） ★★★ | ６ | 大阪府立高校C （Ｒ７年） ★★★ |
下の図のように,∠CAB＝30°,BC＝8cm,AB＝ACの二等辺三角形 ABCがある。点Aから辺BCに垂線ADをひき,∠DBE＝45°となる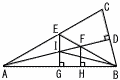 うに辺AC上に点Eをとる。線分ADと線分BEの交点をFとし,点E,点Fから辺ABにそれぞれ垂線 EG,FHをひく。線分ADと線分EGの交点を
I とし,点Bと点 I を結ぶ。(1) 線分AFの長さは( ) cmである。 (2) 線分EFの長さは( ) cmである。 |
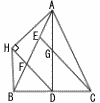 右の図 において,△ABCはAB＝ACの二等辺 三角形である。Dは,△ABCの頂角∠BACの二等分線と辺BCとの交点である。E,Fは辺AB上にあ
ってA,Bと異なる点であり,AE＝EF＝FBである。CとEとを結ぶ。Gは,線分ECと線分ADとの交点である。Hは,Aから直線FDにひいた垂線と直線FDとの交点
である。Hは,直線ABについてCと反対側にある。H とBとを結ぶ。(1) △ABCの内角∠BACの大きさをa°とするとき,△ABCの頂点Cにおける外角の大きさをaを用いて表しなさい。 (2) △AHD∽△CDGであることを証明しなさい。 (3) AB＝7cm,BC＝6cmであるとき, ① 線分GCの長さを求めなさい。 ② △AHBの面積を求めなさい。 |
||
| ３ | 中央大附属高校 （Ｒ７年） ★★★ | ||
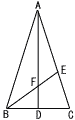 図のように,二等辺三角形ABCの頂角∠Aの二等分線と辺BCの交点をD,底角∠Bの二等分線と辺ACの交点をE,直線ADとBEとの交点をFとする。AB＝2√5,∠Bが∠Aの2倍の大きさのとき,(1) ∠BECの大きさを求めなさい。 (2) 線分BCの長さを求めなさい。 |
|||
| ４ | 盈進高校 （Ｒ６年） ★ | (2) 辺CFの長さを求めなさい。 (3) △CFGの面積がxcm2であるとき,△CDEの面積をxを用いて表しなさい。 |
|
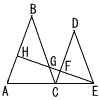 △ABCは,AB＝CB＝6cmの二等辺三角形,△CDEは,CD＝ED＝4cmの二等辺三角形であり,この2つの三角形は相似である。また,A,C,EとE,F,G,Hは,それぞれ同一直線上にあるものとする。CG＝1cmのとき,(1) △CFGと△DFEの面積比を求めなさい。 (右へつづく→) |
|||
