| �P�Q�@�ӎO�p�`�@�i�����j | ||
| �P�Q�@�ӎO�p�`�@�i�����j | ||
| �P | �m�i�w�����Z�@�i�q�T�N�j�@���� | �T | ��@���Z�@�i�q�T�N�j�@���� |
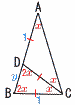 �@���̂悤��AB��AC,BC��AD��CD,BC��1cm�̐}�`������܂��B �@���̂悤��AB��AC,BC��AD��CD,BC��1cm�̐}�`������܂��B(1) ��ADC�̑傫�������߂Ȃ����B �y���z��A��x�Ƃ��� ��ABC��,x�{2x�{2x��180���Cx��36�� �@��ADC��180�|36�~2��108�� (2) BD�̒��������߂Ȃ����B �y���z��CBD�䁢ABC BD��y�Ƃ����, y:1��1:(1�{y)��, y�i1�{y�j��1 �@y2�{y�|1��0���, BD��y��(��5�|1)/2cm (3) AC�̒��������߂Ȃ����B �y���z AC��1�{y��(��5�{1)/2cm |
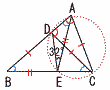 �@�E�̐}�ɂ�����,BD��DC��CA,BE��EA�ł���B��DEA�̑傫����32�x�̂Ƃ�,��ABC�̑傫����(�@)�x�ł���B �@�E�̐}�ɂ�����,BD��DC��CA,BE��EA�ł���B��DEA�̑傫����32�x�̂Ƃ�,��ABC�̑傫����(�@)�x�ł���B�y���z ��DBC�͓ӎO�p�`(��B����D) ��EAB�͓ӎO�p�`(��A����B) �@�����,��DAE����DCE��, ��CAD(�ӎO�p�`)��,��C����ADE��32�� �@��CDA��(180�|32)��2��74�� ��DAB(�ӎO�p�`)��, ��ABC��74��2��37�x |
||
| �Q | ��t�������Z�@�i�q�V�N�j�@������ | �U | ���{�����ZC�@�i�q�V�N�j�@������ |
�@���̐}�̂悤��,��CAB��30��,BC��8cm,AB��AC�̓ӎO�p�` ABC������B�_A�����BC�ɐ���AD���Ђ�,��DBE��45���ƂȂ�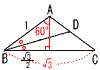 ���ɕ�AC��ɓ_E���Ƃ�B����AD�Ɛ���BE�̌�_��F�Ƃ�,�_E,�_F�����AB�ɂ��ꂼ�ꐂ�� EG,FH���Ђ��B����AD�Ɛ���EG�̌�_��
I �Ƃ�,�_B�Ɠ_ I �����ԁB ���ɕ�AC��ɓ_E���Ƃ�B����AD�Ɛ���BE�̌�_��F�Ƃ�,�_E,�_F�����AB�ɂ��ꂼ�ꐂ�� EG,FH���Ђ��B����AD�Ɛ���EG�̌�_��
I �Ƃ�,�_B�Ɠ_ I �����ԁB(1) ����AF�̒�����(�@�@�@) cm�ł���B �y���z��I BD��30��,60��,90����, I B��I A��8, I D��4 AF��I A�{I F��8�{(4 (2) ����EF�̒�����(�@�@�@) cm�ł���B �y���zI F��IJ EF:FB��IJ:(BI�|IJ)��(4 EF:4 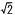 �� �� |
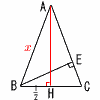 �@�E�̐} �ɂ�����,��ABC��AB��AC�̓� �O�p�`�ł���BD��,��ABC�̒��p��BAC�̓����ƕ�BC�Ƃ̌�_�ł���BE,F�͕�AB��ɂ�
����A,B�ƈقȂ�_�ł���,AE��EF��FB�ł���BC��E�Ƃ����ԁBG��,����EC�Ɛ���AD�Ƃ̌�_�ł���BH��,A���璼��FD�ɂЂ��������ƒ���FD�Ƃ̌�_
�ł���BH��,����AB�ɂ���C�Ɣ��Α��ɂ���BH ��B�Ƃ����ԁB �@�E�̐} �ɂ�����,��ABC��AB��AC�̓� �O�p�`�ł���BD��,��ABC�̒��p��BAC�̓����ƕ�BC�Ƃ̌�_�ł���BE,F�͕�AB��ɂ�
����A,B�ƈقȂ�_�ł���,AE��EF��FB�ł���BC��E�Ƃ����ԁBG��,����EC�Ɛ���AD�Ƃ̌�_�ł���BH��,A���璼��FD�ɂЂ��������ƒ���FD�Ƃ̌�_
�ł���BH��,����AB�ɂ���C�Ɣ��Α��ɂ���BH ��B�Ƃ����ԁB(1) ��ABC�̓��p��BAC�̑傫���� a���Ƃ���Ƃ�,��ABC�̒��_C�ɂ�����O�p�̑傫����a��p���ĕ\���Ȃ����B �y���z�O�p����A�{��B��a�{ (2) ��AHD�䁢CDG�ł��邱�Ƃ��ؖ����Ȃ����B �y�ؖ��z��AHD�Ɓ�CDG��, ��H����D��90���c�A EC �A�C���,2�p������,��AHD�䁢CDG (3) AB��7cm,BC��6cm�ł���Ƃ�, �@ ����GC�̒��������߂Ȃ����B �@ �y���z��ABC��,AD����72�|32��2 ��GCD��,GC����10�{9����19cm 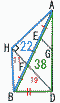 �A ��AHB�̖ʐς����߂Ȃ����B �A ��AHB�̖ʐς����߂Ȃ����B�y���z ��AHD:��CDG:��BHD��40:19:20 ��ADB��38���,��AHB��60�|38��22 ��AHB��(11/19)��ADB��3 |
||
| �R | �����啍�����Z�@�i�q�V�N�j�@���� | ||
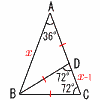 �@�}�̂悤��,�ӎO�p�`ABC�̒��p��A�̓����ƕ�BC�̌�_��D,��p��B�̓����ƕ�AC�̌�_��E,����AD��BE�Ƃ̌�_��F�Ƃ���BAB��2 �@�}�̂悤��,�ӎO�p�`ABC�̒��p��A�̓����ƕ�BC�̌�_��D,��p��B�̓����ƕ�AC�̌�_��E,����AD��BE�Ƃ̌�_��F�Ƃ���BAB��2(1) ��BEC�̑傫�������߂Ȃ����B �y���z�Z��180��5��36�� ��BCE��,��BEC��36�~2��72�� (2) ����BC�̒��������߂Ȃ����B �y���zBC��BE��AE��x�Ƃ����,��ABC�䁢BCE���, �@2 �@BC��x��5�| |
|||
| �S | �m�i���Z�@�i�q�U�N�j�@�� | (2) ��CF�̒��������߂Ȃ����B �y���z(1)���,CF:DF��1:4 CF��4�~ (3) ��CFG�̖ʐς�xcm2�ł���Ƃ�,��CDE�̖ʐς�x��p���ĕ\���Ȃ����B �y���z(1)���,��DFE��16x CD�� |
|
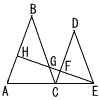 �@��ABC��,AB��CB��6cm�̓ӎO�p�`,��CDE��,CD��ED��4cm�̓ӎO�p�`�ł���,����2�̎O�p�`�͑����ł���B�܂�,A,C,E��E,F,G,H��,���ꂼ�ꓯ�꒼����ɂ�����̂Ƃ���BCG��1cm�̂Ƃ�, �@��ABC��,AB��CB��6cm�̓ӎO�p�`,��CDE��,CD��ED��4cm�̓ӎO�p�`�ł���,����2�̎O�p�`�͑����ł���B�܂�,A,C,E��E,F,G,H��,���ꂼ�ꓯ�꒼����ɂ�����̂Ƃ���BCG��1cm�̂Ƃ�,(1) ��CFG�Ɓ�DFE�̖ʐϔ�����߂Ȃ����B �y���zBC//DE���,��CFG�䁢DFE(������1:4) ��CFG�F��DFE��12:42��1:16 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@(�E�ւÂ���) |
|||