 図形 |
１１ 正三角形 | 月 日（ ） |
| 図形 |
１１ 正三角形 | 月 日（ ） |
| １ | 日大習志野高校 （Ｒ７年） ★★★ | ４ | 滋賀県立膳所高校 （Ｒ５年） ★★ |
 右図のように,１辺の長さが9cmの正三角形ABCがある。3点D,E,Fをそれぞれ辺AB,BC,CA上にとる。AD＝BE＝CF＝5cmのとき,(1) △ADFの面積を求めなさい。 (2) △DEFの面積を求めなさい。 (3) 線分AEとBFの交点をG,BFとCDの交点をH,CDとAEの交点を I とする。△GHI の面積を求めなさい。 |
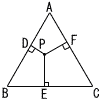 図のように,1辺の長さが6の正三角形ABCの内部にある点Pから各辺に垂線PD,PE,PFをおろす。点Pがどこにあっても,長さの和 PD＋PE＋PF
が一定であることを証明し,その長さの和を求めなさい。 |
||
| ５ | 城北高校 （Ｒ５年） ★★ | ||
 右の図は面積が の正三角形ABCである。線分の長さの和 DE＋DF を求めよ。 |
|||
| ２ | 大分県立高校 （Ｒ７年） ★★★ | ６ | 須磨学園高校 （Ｒ７年） ★★ |
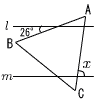
| 右の図のような四角形ABCDがあり, △ACDは正三角形である。 また,点Pは△ABCの内部にあり, △APQが正三角形となるように点Qをとる。ただし,点Qは△ACDの内部にあるものとする。 AC＝5cm,BC＝4cm,∠ACB＝30°とし,線分APと線分BPと線分CPの長きの和をAP＋BP＋CPと表す。 このとき,点Pの位置によって変化するAP＋BP＋CPの長さが最も小さくなるように,点Pの位置を定めた。 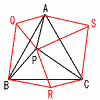 (1) AP＋BP＋CPの長さを求めなさい。 (2) ∠BPCの大きさを求めなさい。 |
 図のように,1辺の長さが16の正三角形ABCがある。線分BC上にAD⊥BCとなるように点Dをとる。このとき,点Dを点Aから線分BCに下ろした垂線の足という。同様に,点Eを点Dから線分ACに下ろした垂線の足,点Fを点Eから線分ABに下ろした垂線の足,点Gを点Fから線分BCに下ろした垂線の足とする。また,線分ADと線分EFの交点を点Pとする。(1) 線分ADの長さを求めなさい。 (2) 線分EPの長さを求めなさい。 (3) 四角形FGDPの面積を求めなさい。 Bを通って四角形FGDPの面積を2等分する直線をl とする。直線l と線分FGとの交点を点H,直線l と線分PDとの交点を点I とする。 (4) 線分DI の長さと線分GHの長さの比DI：GHを最も簡単な整数の比で表しなさい。 (5) 線分DI の長さを求めなさい。 |
||
| ３ | 桜美林高校 （Ｒ６年） ★★★ | ||
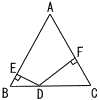
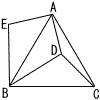 図のような,正三角形ABCがある。△ABCの内部に点Dを,△ABCの外部に点Eを,△BCD≡△BAE となるようにとる。AD＝4cm,BD＝6cm,∠EAD＝90°のとき, (1) ∠EBD の大きさを求めなさい。 (2) 線分AEの長さを求めなさい。 (3) △ADCの面積を求めなさい。 |
|||
