| 10 内心と内接円 | 月 日( ) |
| 10 内心と内接円 | 月 日( ) |
| 1 | 明治大付属明治高校 (R5年) ★★ | 5 | 開成高校 (R5年) ★★★ |
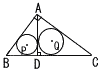 右の図のように,∠A=90°の直角三角形ABCがある。Aから辺BCに垂線をひき,その交点をDとし,△ABD,△ACDの内接円の中心をそれぞれP,Qとする。
BC=a,CA=b,AB=c,△ABCの内接円の半径をrとするとき, 右の図のように,∠A=90°の直角三角形ABCがある。Aから辺BCに垂線をひき,その交点をDとし,△ABD,△ACDの内接円の中心をそれぞれP,Qとする。
BC=a,CA=b,AB=c,△ABCの内接円の半径をrとするとき,(1) rをa,b,cを用いて表せ。 (2) △ACDの内接円の半径をa,b,rを用いて表せ。 (3) 線分PQの長さをrを用いて表せ。 |
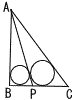 ∠Bが直角である三角形ABCがある。∠BACの二等分線と辺BCの交点をPとおく。 ∠Bが直角である三角形ABCがある。∠BACの二等分線と辺BCの交点をPとおく。AB=2√2,BP=1であるとき, (1) AC,PCの長さをそれぞれ求めよ。 (2) △PAB,△PACの内接円の半径の比を求めよ。 |
||
| 2 | 初芝橋本高校 (R7年) ★ | 6 | 鎌倉学園高校 (R7年) ★★★ |
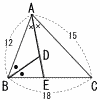 右の図の△ABCにおいて∠Aの二等分綻と辺BCの交点をE,∠Bの二等分綻とAEの交点をDとする。このときAD:DEを求めなさい。 右の図の△ABCにおいて∠Aの二等分綻と辺BCの交点をE,∠Bの二等分綻とAEの交点をDとする。このときAD:DEを求めなさい。 |
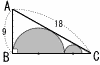 図のように,∠ABC=90°AB=9,AC=18である直角三角形があり,半円が2つ接しています。また,半円どうしも接しています。 図のように,∠ABC=90°AB=9,AC=18である直角三角形があり,半円が2つ接しています。また,半円どうしも接しています。この2つの半円の面積の和を求めなさい。 |
||
| 3 | 國學院大久我山高校 (R6年) ★★ | 7 | 和洋国府台女子高校 (R6年) ★ |
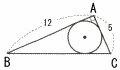 右の図のような∠A=90°,AB=12,AC=5の直角三角形ABCがある。この三角形の3つの辺すべてに接する円の半径は[ ]である。 右の図のような∠A=90°,AB=12,AC=5の直角三角形ABCがある。この三角形の3つの辺すべてに接する円の半径は[ ]である。 |
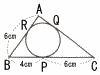 右の図のように,△ABCに内接する円があり,辺BC,CA,ABとの接点を,それぞれP,Q,Rとする。このとき,内接する円の半径を求めよ。 右の図のように,△ABCに内接する円があり,辺BC,CA,ABとの接点を,それぞれP,Q,Rとする。このとき,内接する円の半径を求めよ。 |
||
| 4 | 愛光高校 (R7年) ★★ | 8 | 桐蔭学園高校 (R7年) ★ |
| AB=AC=13,BC=10である△ABCがある。頂点A,B,Cを通る円の半径は[ア ]で,辺AB,BC,CAに接する円の半径は[イ ]である。 |
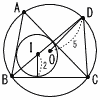 右の図のように,三角形ABCに内接している円Oがあり,その円Oと三角形の辺AB,BC,CAの接点をそれぞれD,E,Fとする。∠CAB=40°,∠BCA=60°のとき,弧の長さの比は,弧DE:弧EF:弧ED=[ア:イ:ウ]である。 右の図のように,三角形ABCに内接している円Oがあり,その円Oと三角形の辺AB,BC,CAの接点をそれぞれD,E,Fとする。∠CAB=40°,∠BCA=60°のとき,弧の長さの比は,弧DE:弧EF:弧ED=[ア:イ:ウ]である。 |
||