| 11 正三角形 (略解) | ||
| 11 正三角形 (略解) | ||
| 1 | 日大習志野高校 (R7年) ★★★ | 4 | 滋賀県立膳所高校 (R5年) ★★ | ||||||||||
 右図のように,1辺の長さが9cmの正三角形ABCがある。3点D,E,Fをそれぞれ辺AB,BC,CA上にとる。AD=BE=CF=5cmのとき, 右図のように,1辺の長さが9cmの正三角形ABCがある。3点D,E,Fをそれぞれ辺AB,BC,CA上にとる。AD=BE=CF=5cmのとき,(1) △ADFの面積を求めなさい。 【解】△ABC= △ADF=△ABC× (2) △DEFの面積を求めなさい。 【解】△DEF=△ABC−3△ADF= (3) 線分AEとBFの交点をG,BFとCDの交点をH,CDとAEの交点を I とする。△GHI の面積を求めなさい。 【解】メネラウスの定理(右下隅参照)より,AG:GE=36:25 △ABG=△BCH=△CAI = △GHI ={1−(20/61)×3}△ABC=(1/61)× |
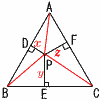 長さの和 PD+PE+PF が一定であることを証明し,その長さの和を求めなさい。 長さの和 PD+PE+PF が一定であることを証明し,その長さの和を求めなさい。【解】右上図参照 1辺6の△ABC= =△PAB+△PBC+△PCA 3(x+y+z)=9 |
||||||||||||
| 5 | 城北高校 (R5年) ★★ | ||||||||||||
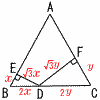 右の図は面積が 右の図は面積が【解】△ABCの1辺をaとすると △ABC= BC=2(x+y)=2で,x+y=1 よって, DE+DF= |
|||||||||||||
| 2 | 大分県立高校 (R7年) ★★ | 6 | 須磨学園高校 (R7年) ★★ | ||||||||||
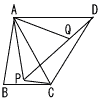 右の図のような四角形ABCDがあり, △ACDは正三角形である。 また,点Pは△ABCの内部にあり, △APQが正三角形となるように点Qをとる。ただし,点Qは△ACDの内部にあるものとする。 右の図のような四角形ABCDがあり, △ACDは正三角形である。 また,点Pは△ABCの内部にあり, △APQが正三角形となるように点Qをとる。ただし,点Qは△ACDの内部にあるものとする。AC=5cm,BC=4cm,∠ACB=30°とし,線分APと線分BPと線分CPの長きの和をAP+BP+CPと表す。 このとき,点Pの位置によって変化するAP+BP+CPの長さが最も小さくなるように,点Pの位置を定めた。 (1) AP+BP+CPの長さを求めなさい。 【解】△APC≡△AQD(2辺夾角相等)より,CP=DQ 最短はBDが一直線になるときで, AP+BP+CP=AQ+BP+DQ=BD=√42+52=√41 (2) ∠BPCの大きさを求めなさい。 【解】∠APC=∠AQD=120°より,∠QPC=60° ∠BPC=180−60=120° |
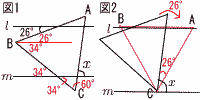
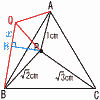 図のように,1辺の長さが16の正三角形ABCがある。線分BC上にAD⊥BCとなるように点Dをとる。 このとき,点Dを点Aから線分BCに下ろした垂線の足という。同様に,点Eを点Dから線分ACに下ろした垂線の足,点Fを点Eから線分ABに下ろした垂線の足,点Gを点Fから線分BCに下ろした垂線の足とする。
また,線分ADと線分EFの交点を点Pとする。 図のように,1辺の長さが16の正三角形ABCがある。線分BC上にAD⊥BCとなるように点Dをとる。 このとき,点Dを点Aから線分BCに下ろした垂線の足という。同様に,点Eを点Dから線分ACに下ろした垂線の足,点Fを点Eから線分ABに下ろした垂線の足,点Gを点Fから線分BCに下ろした垂線の足とする。
また,線分ADと線分EFの交点を点Pとする。(1) 線分ADの長さを求めなさい。 【解】△ACDで,AD= (2) 線分EPの長さを求めなさい。 【解】△EPDは正三角形で,EP=ED=4 (3) 四角形FGDPの面積を求めなさい。 【解】四角形FGDP= 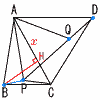 Bを通って四角形FGDPの面積を2等分する直線をl とする。直線l と線分FGとの交点を点H,直線l と線分PDとの交点を点i とする。 Bを通って四角形FGDPの面積を2等分する直線をl とする。直線l と線分FGとの交点を点H,直線l と線分PDとの交点を点i とする。(4) 線分DI の長さと線分GHの長さの比DI:GHを最も簡単な整数の比で表しなさい。 【解】l はFDとGPの交点を通る △BDI∽△BGHより, DI:GH=BD:BG=8:5 (5) 線分DI の長さを求めなさい。 【解】 (39/64)△BDI=
|
||||||||||||
| 3 | 桜美林高校 (R6年) ★★★ | ||||||||||||
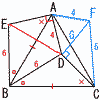 図のような,正三角形ABCがある。△ABCの内部に点Dを,△ABCの外部に点Eを,△BCD≡△BAE となるようにとる。 図のような,正三角形ABCがある。△ABCの内部に点Dを,△ABCの外部に点Eを,△BCD≡△BAE となるようにとる。AD=4cm,BD=6cm,∠EAD=90°のとき, (1) ∠EBD の大きさを求めなさい。 【解】△BAE≡△BCDより,∠EBA=∠DBC ∠EBD=∠EBA+∠ABD=∠ABC=60° (2) 線分AEの長さを求めなさい。 【解】△EBDは正三角形で,ED=6 △AEDで,AE=√62−42=2√5cm 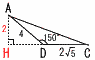 (3) △ADCの面積を求めなさい。 (3) △ADCの面積を求めなさい。【解】△ABD≡△ACFとなる点Fをとると, ∠ADC=60+90=150°(左図の青) 右図のような△AHDを考えて,AH=2 △ADC= |
|||||||||||||