| Ѓ@‚XЃ@“с‚В‚М‰~ | Ѓ@Ѓ@Ѓ@ЊҺЃ@Ѓ@Ѓ@“ъЃiЃ@Ѓ@Ѓj |
| Ѓ@‚XЃ@“с‚В‚М‰~ | Ѓ@Ѓ@Ѓ@ЊҺЃ@Ѓ@Ѓ@“ъЃiЃ@Ѓ@Ѓj |
| ‚P | ‹ЛЊхЉw‰ЂҚ‚ҚZЃ@Ѓi‚q‚T”NЃjЃ@ЃљЃљ | ‚S | ‹ЛЊхЉw‰ЂҚ‚ҚZЃ@Ѓi‚q‚V”NЃjЃ@ЃљЃљ |
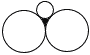 Ѓ@ђ}‚̂悤‚Й”әЊa‚Ғ‚»‚к‚ә‚к1,1,Ѓг2Ѓ|1‚Е‚ ‚й‚R‚В‚М‰~‚ҒЉOђЪ‚µ‚Д‚ұ‚йЃB‚±‚М‚Ж‚«,3‚В‚М‰~‚Е€Н‚Ь‚к‚Ңђ}Њ`‚М–КђП‚р‹Ѓ‚Я‚жЃB Ѓ@ђ}‚̂悤‚Й”әЊa‚Ғ‚»‚к‚ә‚к1,1,Ѓг2Ѓ|1‚Е‚ ‚й‚R‚В‚М‰~‚ҒЉOђЪ‚µ‚Д‚ұ‚йЃB‚±‚М‚Ж‚«,3‚В‚М‰~‚Е€Н‚Ь‚к‚Ңђ}Њ`‚М–КђП‚р‹Ѓ‚Я‚жЃBЃ@ |
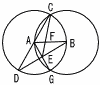 Ѓ@ђ}‚̂悤‚Й,ҺlЉpЊ`ABCD‚НЃЪCЃЃЃЪDЃЃ90Ѓ‹‚М‘дЊ`‚Е‚ ‚йЃB‰~O‚Н‘дЊ`‚М‚·‚Ч‚Д‚М•У‚ЖђЪ‚µ,‰~O'‚Н•УAB,BC‚Ё‚ж‚Т‰~O‚ЖђЪ‚µ‚Д‚ұ‚йЃBABЃЃ2 Ѓ@ђ}‚̂悤‚Й,ҺlЉpЊ`ABCD‚НЃЪCЃЃЃЪDЃЃ90Ѓ‹‚М‘дЊ`‚Е‚ ‚йЃB‰~O‚Н‘дЊ`‚М‚·‚Ч‚Д‚М•У‚ЖђЪ‚µ,‰~O'‚Н•УAB,BC‚Ё‚ж‚Т‰~O‚ЖђЪ‚µ‚Д‚ұ‚йЃBABЃЃ2Ѓ@ |
||
| ‚Q | “Њ‹һҚH‘е•Қ‘®‰И‹ZҚ‚ҚZЃ@Ѓi‚q‚T”NЃjЃ@ЃљЃљ | ‚T | “Њ‹һ‰ИЉw‘е•Қ‘®‰И‹ZҚ‚ҚZЃ@Ѓi‚q‚V”NЃjЃ@Ѓљ |
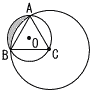 Ѓ@ђ}‚Й‚Ё‚ұ‚Д,3“_A,B,C‚Н‰~O‚МҺьЏг‚Й‚ ‚и,ЃұABC‚Н1•У‚М’·‚і‚Ғ6cm‚МђіҺOЉpЊ`‚Е‚ ‚йЃB‚Ь‚Ң,A,B‚НC‚р’†ђS‚Ж‚·‚й‰~‚МҺьЏг‚Й‚ ‚йЃB‚±‚М‚Ж‚«,‰e‚р‚В‚Ү‚Ң•”•Ғ‚М–КђП‚р‹Ѓ‚Я‚И‚і‚ұЃB Ѓ@ђ}‚Й‚Ё‚ұ‚Д,3“_A,B,C‚Н‰~O‚МҺьЏг‚Й‚ ‚и,ЃұABC‚Н1•У‚М’·‚і‚Ғ6cm‚МђіҺOЉpЊ`‚Е‚ ‚йЃB‚Ь‚Ң,A,B‚НC‚р’†ђS‚Ж‚·‚й‰~‚МҺьЏг‚Й‚ ‚йЃB‚±‚М‚Ж‚«,‰e‚р‚В‚Ү‚Ң•”•Ғ‚М–КђП‚р‹Ѓ‚Я‚И‚і‚ұЃBЃ@ |
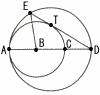 Ѓ@ђ}‚̂悤‚Й,4“_A,B,C,D‚Н€к’әђьЏг‚Й‚ ‚и,ABЃЃBCЃЃCDЃЃ1cm‚Ж‚·‚йЃB“_E‚Нђь•ҒAD‚р’әЊa‚Ж‚·‚й‰~‚МҺьЏг‚Й‚ ‚и,ђь•ҒED‚Нђь•ҒAC‚р’әЊa‚Ж‚·‚й‰~‚Ж“_‚s‚ЕђЪ‚µ‚Д‚ұ‚йЃB‚±‚М‚Ж‚«,ђь•ҒBE‚М’·‚і‚р‹Ѓ‚Я‚И‚і‚ұЃB Ѓ@ђ}‚̂悤‚Й,4“_A,B,C,D‚Н€к’әђьЏг‚Й‚ ‚и,ABЃЃBCЃЃCDЃЃ1cm‚Ж‚·‚йЃB“_E‚Нђь•ҒAD‚р’әЊa‚Ж‚·‚й‰~‚МҺьЏг‚Й‚ ‚и,ђь•ҒED‚Нђь•ҒAC‚р’әЊa‚Ж‚·‚й‰~‚Ж“_‚s‚ЕђЪ‚µ‚Д‚ұ‚йЃB‚±‚М‚Ж‚«,ђь•ҒBE‚М’·‚і‚р‹Ѓ‚Я‚И‚і‚ұЃBЃ@ |
||
| ‚R | ‹Л•ьҚ‚ҚZЃ@Ѓi‚q‚U”NЃjЃ@ЃљЃљЃљ | ‚U | “ЊЉCҚ‚ҚZЃ@Ѓi‚q‚S”NЃjЃ@ЃљЃљЃљ |
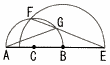 Ѓ@‰E‚Мђ}‚̂悤‚Й“_‚b‚р’†ђS‚Ж‚µ,ђь•ҒAB‚р’әЊa‚Ж‚·‚й”ә‰~‚Ж,“_‚a‚р’†ђS‚Ж‚µ,ђь•ҒDE‚р’әЊa‚Ж‚·‚й”ә‰~‚Ғ‚ ‚йЃB Ѓ@‰E‚Мђ}‚̂悤‚Й“_‚b‚р’†ђS‚Ж‚µ,ђь•ҒAB‚р’әЊa‚Ж‚·‚й”ә‰~‚Ж,“_‚a‚р’†ђS‚Ж‚µ,ђь•ҒDE‚р’әЊa‚Ж‚·‚й”ә‰~‚Ғ‚ ‚йЃBЃ@‚Ң‚ң‚µ,D‚Нђь•ҒACЏг‚М“_‚Е‚ ‚йЃB (1) GAЃЃGE‚Е‚ ‚й‚±‚Ж‚рЏШ–ң‚№‚жЃB (2) ACЃЃ5,BEЃЃ8‚М‚Ж‚«,Һџ‚М‚а‚М‚р‹Ѓ‚Я‚жЃB ‡@ ЃұCBF‚М–КђП ‡A EF‚М’·‚і ‡B ЃұGAE‚М–КђП Ѓ@ |
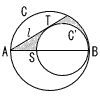 Ѓ@’·‚і‚Ғ6cm‚Мђь•ҒAB‚р’әЊa‚Ж‚·‚й‰~C‚Ж,‰~C‚ЙB‚Е“ађЪ‚·‚й”әЊa2cm‚М‰~C'‚Ғ‚ ‚йЃB“_A‚©‚з‰~C'‚Й€ш‚ұ‚ҢђЪђь‚рl,ђь•ҒAB‚Ж‰~C'‚М“_B€ИЉO‚М‹¤—L“_‚рS,ђЪђьl‚Ж‰~C'‚МђЪ“_‚рT‚Ж‚·‚й‚Ж‚«, Ѓ@’·‚і‚Ғ6cm‚Мђь•ҒAB‚р’әЊa‚Ж‚·‚й‰~C‚Ж,‰~C‚ЙB‚Е“ађЪ‚·‚й”әЊa2cm‚М‰~C'‚Ғ‚ ‚йЃB“_A‚©‚з‰~C'‚Й€ш‚ұ‚ҢђЪђь‚рl,ђь•ҒAB‚Ж‰~C'‚М“_B€ИЉO‚М‹¤—L“_‚рS,ђЪђьl‚Ж‰~C'‚МђЪ“_‚рT‚Ж‚·‚й‚Ж‚«,(1) ‰~C,‰~C',ђЪђьl‚Е€Н‚Ь‚к‚ҢҺОђь•”‚М–КђП‚Н[Ѓ@Ѓ@]cm2‚Е‚ ‚йЃB (2) ’әђьST‚Ж‰~C‚М2‚В‚МЊр“_‚рЊ‹‚с‚ңђь•Ғ‚М’·‚і‚Н[Ѓ@Ѓ@]cm‚Е‚ ‚йЃB Ѓ@ |
||
| ‚V | “y‰Y“ъ‘еҚ‚ҚZЃ@Ѓi‚q‚V”NЃjЃ@Ѓљ | ||
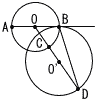 Ѓ@ђь•ҒAB‚р’әЊa‚Ж‚·‚й‰~O‚Ж,’әђьAB‚Ж“_B‚ЕђЪ‚·‚й‰~O'‚Ғ‚ ‚и,’әђьOO'‚Ж‰~O,‰~O'‚Ж‚МЊр“_‚рђ}‚̂悤‚Й‚»‚к‚ә‚кC,D‚Ж‚·‚йЃBЃЪBDCЃЃ18Ѓ‹‚М‚Ж‚«,ЃЪBOЃЃ[ѓAЃ@]Ѓ‹,ЃЪCBDЃЃ[ѓCЃ@]Ѓ‹‚Е‚ ‚йЃB Ѓ@ђь•ҒAB‚р’әЊa‚Ж‚·‚й‰~O‚Ж,’әђьAB‚Ж“_B‚ЕђЪ‚·‚й‰~O'‚Ғ‚ ‚и,’әђьOO'‚Ж‰~O,‰~O'‚Ж‚МЊр“_‚рђ}‚̂悤‚Й‚»‚к‚ә‚кC,D‚Ж‚·‚йЃBЃЪBDCЃЃ18Ѓ‹‚М‚Ж‚«,ЃЪBOЃЃ[ѓAЃ@]Ѓ‹,ЃЪCBDЃЃ[ѓCЃ@]Ѓ‹‚Е‚ ‚йЃBЃ@ |
|||
ЃmTOPЃnЃmBACKЃnЃmNEXTЃnЃm‰р“љЃnЃ@Ѓ@Ѓљ’† ЃљЃљ‚в‚в“п ЃљЃљЃљ“пЃ@![]() €уҚь—p
€уҚь—p