| Ѓ@‚WЃ@‰~‚ЖђЪђь | Ѓ@Ѓ@Ѓ@ЊЋЃ@Ѓ@Ѓ@“ъЃiЃ@Ѓ@Ѓj |
| Ѓ@‚WЃ@‰~‚ЖђЪђь | Ѓ@Ѓ@Ѓ@ЊЋЃ@Ѓ@Ѓ@“ъЃiЃ@Ѓ@Ѓj |
| ‚P | ’}”g‘е•Ќ‘®Ќ‚ЌZЃ@Ѓi‚q‚T”NЃjЃ@ЃљЃљЃљ | ‚S | ЋsђмЌ‚ЌZЃ@Ѓi‚q‚V”NЃjЃ@ЃљЃљЃљ | |
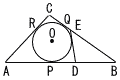 Ѓ@‰E‚Мђ}‚̂悤‚Й,’·‚і‚Є14cm‚Мђь•ЄABЏг‚Й“_P‚р‚Ж‚йЃB‚Ѕ‚ѕ‚µ,APЃѓBP‚Ж‚·‚йЃBP‚Еђь•ЄAB‚ЖђЪ‚·‚й‰~‚O‚Й,2“_B,A‚©‚з‚»‚к‚ј‚к“_Q,R‚ЕђЪ‚·‚йђЪђь‚р€ш‚«,‚»‚М2–{‚МђЪђь‚МЊр“_‚рC‚Ж‚·‚й‚Ж,BCЃЃ10cm‚Ж‚И‚Б‚ЅЃB Ѓ@‰E‚Мђ}‚̂悤‚Й,’·‚і‚Є14cm‚Мђь•ЄABЏг‚Й“_P‚р‚Ж‚йЃB‚Ѕ‚ѕ‚µ,APЃѓBP‚Ж‚·‚йЃBP‚Еђь•ЄAB‚ЖђЪ‚·‚й‰~‚O‚Й,2“_B,A‚©‚з‚»‚к‚ј‚к“_Q,R‚ЕђЪ‚·‚йђЪђь‚р€ш‚«,‚»‚М2–{‚МђЪђь‚МЊр“_‚рC‚Ж‚·‚й‚Ж,BCЃЃ10cm‚Ж‚И‚Б‚ЅЃBЃ@‚Ь‚Ѕ,ђь•ЄABЏг‚ЙBDЃЃ5cm‚Ж‚И‚й“_D‚р‚Ж‚и,D‚©‚з‰~O‚Й€ш‚ў‚ЅђЪђь‚Жђь•ЄBC‚Ж‚МЊр“_‚рE‚Ж‚·‚й‚Ж,BEЃЃ7cm‚Ж‚И‚Б‚ЅЃB (1) ђь•ЄAC‚М’·‚і‚Н,ђь•ЄDE‚М’·‚і‚М(Ѓ@)”{‚Е‚ ‚йЃB (2) ђь•ЄAR‚М’·‚і‚Н,ARЃЃ(Ѓ@)cm‚Е‚ ‚йЃB (3) ђь•ЄAE,CD‚МЊр“_‚рF‚Ж‚·‚й‚Ж‚«,A‚e:‚eE‚рЌЕ‚аЉИ’P‚Иђ®ђ”‚М”д‚Е•\‚·‚Ж,AF:FEЃЃ(Ѓ@):(Ѓ@)‚Е‚ ‚йЃB Ѓ@ |
Ѓ@Ћџ‚Мђ}‚Є€И‰є‚МЏрЊЏ‚р–ћ‚Ѕ‚µ‚Д‚ў‚й‚Ж‚«,
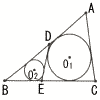 (1) ‰~O1‚М”јЊa‚р‹Ѓ‚Я‚жЃB (1) ‰~O1‚М”јЊa‚р‹Ѓ‚Я‚жЃB(2) ‰~O2‚М”јЊa‚р‹Ѓ‚Я‚жЃB (3) ЋlЉpЊ`DBEO1‚М–КђП‚р‹Ѓ‚Я‚жЃB Ѓ@ |
|||
| ‚Q | –@ђ‘е‘ж“сЌ‚ЌZЃ@Ѓi‚q‚V”NЃjЃ@ЃљЃљЃљ | ‚T | ђВ‰_Ќ‚ЌZЃ@Ѓi‚q‚V”NЃjЃ@ЃљЃљЃљ | |
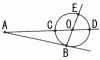 Ѓ@ђ}‚̂悤‚И“_O‚р’†ђS‚Ж‚·‚й”јЊa1cm‚М‰~‚Є‚ ‚йЃB‰~‚МЉO‚Й‚ ‚й“_‚`‚©‚з‰~‚ЙђЪђь‚р€ш‚«,‚»‚МђЪ“_‚р“_B‚Ж‚·‚йЃB‚Ь‚Ѕ,”ј’јђьAO‚Ж‰~‚МЊр“_‚р“_A‚Й‹Я‚ў“_‚©‚з‚»‚к‚ј‚к“_C,“_D‚Ж‚µ,”ј’јђьBO‚Ж‰~‚МЊр“_‚р“_E‚Ж‚·‚йЃBOC:CAЃЃ1:3‚М‚Ж‚«, Ѓ@ђ}‚̂悤‚И“_O‚р’†ђS‚Ж‚·‚й”јЊa1cm‚М‰~‚Є‚ ‚йЃB‰~‚МЉO‚Й‚ ‚й“_‚`‚©‚з‰~‚ЙђЪђь‚р€ш‚«,‚»‚МђЪ“_‚р“_B‚Ж‚·‚йЃB‚Ь‚Ѕ,”ј’јђьAO‚Ж‰~‚МЊр“_‚р“_A‚Й‹Я‚ў“_‚©‚з‚»‚к‚ј‚к“_C,“_D‚Ж‚µ,”ј’јђьBO‚Ж‰~‚МЊр“_‚р“_E‚Ж‚·‚йЃBOC:CAЃЃ1:3‚М‚Ж‚«,(1) ЃЪBACЃЃaЃ‹‚Ж‚·‚й‚Ж‚«,ЃЪBCD‚рaЃ‹‚р—p‚ў‚ЅЋ®‚Е•\‚µ‚И‚і‚ўЃB (2) ђь•ЄCE‚М’·‚і‚р‹Ѓ‚Я‚И‚і‚ўЃB (3) ЃўABC‚М–КђП‚р‹Ѓ‚Я‚И‚і‚ўЃB Ѓ@Ѓ@ |
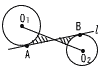 Ѓ@‰є‚Мђ}‚Й‚Ё‚ў‚Д,“_O‚р’†ђS‚Ж‚·‚й”јЊa‚Є1cm‚М‰~‚Ж,“_O'‚р’†ђS‚Ж‚·‚й”јЊa‚Є3cm‚М‰~‚Є“_P‚ЕђЪ‚µ,‚і‚з‚Йђ}‚̂悤‚Й’јђьl ‚Ж‚»‚к‚ј‚к“_Q,“_R‚ЕђЪ‚µ‚Д‚ў‚йЃB‚Ь‚Ѕ,’јђьm‚Н2‚В‚М‰~‚Ж“_P‚ЕђЪ‚µ‚Д‚Ё‚и,’јђьl ‚Жm‚МЊр“_‚рM‚Ж‚·‚йЃB Ѓ@‰є‚Мђ}‚Й‚Ё‚ў‚Д,“_O‚р’†ђS‚Ж‚·‚й”јЊa‚Є1cm‚М‰~‚Ж,“_O'‚р’†ђS‚Ж‚·‚й”јЊa‚Є3cm‚М‰~‚Є“_P‚ЕђЪ‚µ,‚і‚з‚Йђ}‚̂悤‚Й’јђьl ‚Ж‚»‚к‚ј‚к“_Q,“_R‚ЕђЪ‚µ‚Д‚ў‚йЃB‚Ь‚Ѕ,’јђьm‚Н2‚В‚М‰~‚Ж“_P‚ЕђЪ‚µ‚Д‚Ё‚и,’јђьl ‚Жm‚МЊр“_‚рM‚Ж‚·‚йЃB(1) ЃЪPO'R‚М‘е‚«‚і‚р‹Ѓ‚Я‚жЃB (2) ђь•ЄQR‚М’·‚і‚р‹Ѓ‚Я‚жЃB (3) ђь•ЄPMђь•ЄQM‚ЖЊКPQ‚Е€Н‚Ь‚к‚Ѕ•”•Є‚М–КђП‚р‹Ѓ‚Я‚жЃB Ѓ@ |
|||
| ‚R | Џx‘дЌb•{Ќ‚ЌZЃ@Ѓi‚q‚U”NЃjЃ@ЃљЃљ | ‚U | Љ™‘qЉw‰ЂЌ‚ЌZЃ@Ѓi‚q‚U”NЃjЃ@ЃљЃљ | |
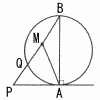 Ѓ@‰Eђ}‚М”јЊa2cm‚М‰~‚Й‚Ё‚ў‚Д,ђь•ЄAB‚Н‰~‚М’јЊa‚Е,’јђьPA‚Н‰~‚МђЪђь‚ЕPAЃЃ3cm‚Е‚ ‚йЃB‚Ь‚Ѕ,’јђьPB‚Є‰~‚ЖЊр‚н‚йB€ИЉO‚М“_‚рQ‚Ж‚µ,ђь•ЄBQ‚М’†“_‚рM‚Ж‚·‚йЃB‚±‚М‚Ж‚«,ЋOЉpЊ`APM‚М–КђП‚р‹Ѓ‚Я‚жЃB Ѓ@‰Eђ}‚М”јЊa2cm‚М‰~‚Й‚Ё‚ў‚Д,ђь•ЄAB‚Н‰~‚М’јЊa‚Е,’јђьPA‚Н‰~‚МђЪђь‚ЕPAЃЃ3cm‚Е‚ ‚йЃB‚Ь‚Ѕ,’јђьPB‚Є‰~‚ЖЊр‚н‚йB€ИЉO‚М“_‚рQ‚Ж‚µ,ђь•ЄBQ‚М’†“_‚рM‚Ж‚·‚йЃB‚±‚М‚Ж‚«,ЋOЉpЊ`APM‚М–КђП‚р‹Ѓ‚Я‚жЃBЃ@ |
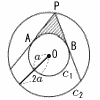 Ѓ@ђ}‚̂悤‚Й’†ђS‚Є“Ї‚¶‚Е”јЊa‚Є‚»‚к‚ј‚кa,2a‚Е‚ ‚й‰~C1,C2‚Є‚ ‚и‚Ь‚·ЃB Ѓ@ђ}‚̂悤‚Й’†ђS‚Є“Ї‚¶‚Е”јЊa‚Є‚»‚к‚ј‚кa,2a‚Е‚ ‚й‰~C1,C2‚Є‚ ‚и‚Ь‚·ЃBЃ@ C2Џг‚М“_P‚©‚зC1‚Й2–{‚МђЪђьPA,PB‚р€ш‚ў‚Ѕ‚Ж‚«,ЋОђь•”•Є‚М–КђП‚р‹Ѓ‚Я‚И‚і‚ўЃB |
|||
ЃmTOPЃnЃmBACKЃnЃmNEXTЃnЃm‰р“љЃnЃ@Ѓ@Ѓљ’† ЃљЃљ‚в‚в“п ЃљЃљЃљ“пЃ@![]() €уЌь—p
€уЌь—p