| �X�@��̉~�@�i�����j | ||
| �X�@��̉~�@�i�����j | ||
| �P | �ˌ��w�����Z�@�i�q�T�N�j�@���� | �S | �ˌ��w�����Z�@�i�q�V�N�j�@���� |
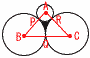 �@�}�̂悤�ɔ��a�����ꂼ��1,1,��2�|1�ł���R�̉~���O�ڂ��Ă���B���̂Ƃ�,3�̉~�ň͂܂ꂽ�}�`�̖ʐς����߂�B �@�}�̂悤�ɔ��a�����ꂼ��1,1,��2�|1�ł���R�̉~���O�ڂ��Ă���B���̂Ƃ�,3�̉~�ň͂܂ꂽ�}�`�̖ʐς����߂�B�y���z3�~A,B,C�̐ړ_��P,Q,R�Ƃ��� �ʐρ���ABC�|(��`APR�{��`BPQ�{��`CQR) �@�� �@��1�| �@��1�{( |
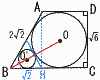 �@�}�̂悤��,�l�p�`ABCD�́�C����D��90���̑�`�ł���B�~O�͑�`�̂��ׂĂ̕ӂƐڂ�,�~O'�͕�AB,BC����҉~O�Ɛڂ��Ă���BAB��2 �@�}�̂悤��,�l�p�`ABCD�́�C����D��90���̑�`�ł���B�~O�͑�`�̂��ׂĂ̕ӂƐڂ�,�~O'�͕�AB,BC����҉~O�Ɛڂ��Ă���BAB��2�y���z ��B��60��,BH�� �~O'��1�� �@���a�� |
||
| �Q | �����H�啍���ȋZ���Z�@�i�q�T�N�j�@���� | �T | �����Ȋw�啍���ȋZ���Z�@�i�q�V�N�j�@�� |
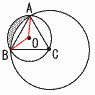 �@�e�����������̖ʐ� �@�e�����������̖ʐ��y���z �~O��,��`OAB��(2��3)2���~ �~C��,��`CAB��62���~ �e��(��`OAB�{ �@��4���{ �@ |
 �@�}�̂悤��,4�_A,B,C,D�͈꒼����ɂ���,AB��BC��CD��1cm�Ƃ���B�_E�͐���AD�a�Ƃ���~�̎���ɂ���,����ED�͐���AC�a�Ƃ���~�Ɠ_�s�Őڂ��Ă���B���̂Ƃ�,����BE�̒��������߂Ȃ����B �@�}�̂悤��,4�_A,B,C,D�͈꒼����ɂ���,AB��BC��CD��1cm�Ƃ���B�_E�͐���AD�a�Ƃ���~�̎���ɂ���,����ED�͐���AC�a�Ƃ���~�Ɠ_�s�Őڂ��Ă���B���̂Ƃ�,����BE�̒��������߂Ȃ����B�y���z ��DTB�䁢DEA(������2:3)���,TE�� ��BTE��,BE����( |
||
| �R | �˕����Z�@�i�q�U�N�j�@������ | �U | ���C���Z�@�i�q�S�N�j�@������ |
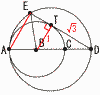
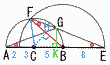 �@�E�̐}�̂悤�ɓ_C�𒆐S�Ƃ�,����AB�a�Ƃ��锼�~��,�_B�𒆐S�Ƃ�,����DE�a�Ƃ��锼�~������B �@�E�̐}�̂悤�ɓ_C�𒆐S�Ƃ�,����AB�a�Ƃ��锼�~��,�_B�𒆐S�Ƃ�,����DE�a�Ƃ��锼�~������B�@������,D�͐���AC��̓_�ł���B (1) GA��GE�ł��邱�Ƃ��ؖ�����B �y�ؖ��z ��A����F(��BG�̉~���p)�c�A ��E����F(���aBE��BF)�@�c�C �A���C���,��A����E��, GA��GE (2) AC��5,BE��8�̂Ƃ�,���̂��̂����߂�B �@ ��CBF�̖ʐ� �y���z����CH�����낷��,BH�� ��CBF�� �A EF�̒��� �y���z��CAG�䁢GAE���,CA:AG��GA:AE �@5:AG��GA:18��,AG��3��10 ��GAE�䁢BEF���,GA�FAE��BE:EF �@3��10:18��8:EF��, EF�� �B ��GAE�̖ʐ� �y���z��GAE�͓ӎO�p�`��,AK��9,GK��3 ��GAE�� |
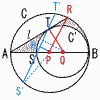 �@������6cm�̐���AB�a�Ƃ���~C��,�~C��B�œ��ڂ��锼�a2cm�̉~C'������B �@������6cm�̐���AB�a�Ƃ���~C��,�~C��B�œ��ڂ��锼�a2cm�̉~C'������B(1) �~C,�~C',�ڐ�l�ň͂܂ꂽ�ΐ�����[�@�@]cm2�ł���B �y���z2�~�̒��S��P,Q�Ƃ����, ��AQT��,��A��30��,��BPR��60�� �ΐ�����(��APR�{��`PBR)�|���~C' �@��( �@�� (2) ����ST�Ɖ~C��2�̌�_���������̒�����[�@�@]cm �y���z ��QST�͐��O�p�`��,PH����3�~ ��S'PT'��,S'T'��2S'H��2���@{32�|( |
||
| �V | �y�Y���卂�Z�@�i�q�V�N�j�@�� | ||
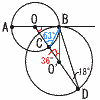 �@����AB�a�Ƃ���~O��,����AB�Ɠ_B�Őڂ���~O'������,����OO'�Ɖ~O,�~O'�Ƃ̌�_��}�̂悤�ɂ��ꂼ��C,D�Ƃ���B��BDC��18���̂Ƃ�,��BOD��[�A�@]��,��CBD��[�C�@]���ł���B �@����AB�a�Ƃ���~O��,����AB�Ɠ_B�Őڂ���~O'������,����OO'�Ɖ~O,�~O'�Ƃ̌�_��}�̂悤�ɂ��ꂼ��C,D�Ƃ���B��BDC��18���̂Ƃ�,��BOD��[�A�@]��,��CBD��[�C�@]���ł���B�y���z �A ��OO'B��,��BOD��180�|(90�{36)��54�� �C �A���,��OCB��63��,��CBD��,��CBD��63�|18��45���@ |
|||