| 7 円と四角形 | 月 日( ) |
| 7 円と四角形 | 月 日( ) |
| 1 | 中大附属高校 (R7年) ★★ | 4 | 西大和学園高校 (R7年) ★★ |
 下の図の△ABC において,BM=MC,∠BAC=52°,BD⊥AC,CE⊥AB である。このとき,∠EMD の大きさを求めなさい。 下の図の△ABC において,BM=MC,∠BAC=52°,BD⊥AC,CE⊥AB である。このとき,∠EMD の大きさを求めなさい。 |
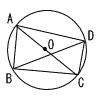
 図において,AB=BC,CD=AE= 図において,AB=BC,CD=AE= |
||
| 2 | 東大寺学園高校 (R5年) ★★★ | 5 | 桐朋高校 (R7年) ★★★ |
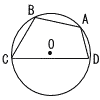 図のように,点Oを中心とする円0の周上に4点A,B,C,Dがあり,AB=BC=6,CD=10,DA=4を満たしている。 図のように,点Oを中心とする円0の周上に4点A,B,C,Dがあり,AB=BC=6,CD=10,DA=4を満たしている。(1) △ABDの面積と△BCDの面積の比を最も簡単な整数の比で表せ。 (2) 線分CD上にCE=6となる点Eをとるとき,△BEDの面積を求めよ。 (3) 線分BDの長さを求めよ。 (4) 円0の半径を求めよ。 |
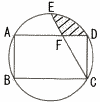 右の図のように,半径1の円に辺ABの長さが1の長方形ABCDが内接している。∠ACDの2等分線と円との交点のうち,Cと異なる方をEとし,直線CEと辺DAとの交点をFとする。 右の図のように,半径1の円に辺ABの長さが1の長方形ABCDが内接している。∠ACDの2等分線と円との交点のうち,Cと異なる方をEとし,直線CEと辺DAとの交点をFとする。(1) BC=ECであることを証明せよ。 (2) 線分EFの長さを求めよ。 (3) 斜線部分の図形の面積を求めよ。 (4) 弧ED上に点Pを弧,EP=弧PDとなるようにとる。斜線部分の図形を直線APで2つに分けたとき,点Eを含む方の図形の面積を求めよ。 |
||
| 3 | 函館ラ・サール高校 (R6年) ★★ | 6 | 明大付属中野高校 (R7年) ★★ |
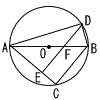
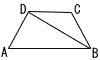 AB= AB=(1) ∠ADBの大きさを求めなさい。 2) DCの長さを求めなさい。 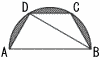 (3) 右の図は,台形ABCDとその台形に外接している円の一部である。図の斜線部分を直線ABを軸に1回転してできる回転体の体積を 求めなさい。 (3) 右の図は,台形ABCDとその台形に外接している円の一部である。図の斜線部分を直線ABを軸に1回転してできる回転体の体積を 求めなさい。 |
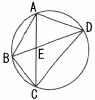 右の図のように,四角形ABCDは,AB=6cm,BC=4cm,CD=12cm,DA=6cmであり,4点A,B,C,Dは1つの円周上にあります。対角線ACとBDの交点をEとするとき, 右の図のように,四角形ABCDは,AB=6cm,BC=4cm,CD=12cm,DA=6cmであり,4点A,B,C,Dは1つの円周上にあります。対角線ACとBDの交点をEとするとき,(1) AE:BEを最も簡単な整数の比で表しなさい。 (2) BE:DEを最も簡単な整数の比で表しなさい。 (3) 対角線BDの長さを求めなさい。 |
||