| 3 線分比・面積比 | 月 日( ) |
| 3 線分比・面積比 | 月 日( ) |
| 1 | 関西学院高等部 (R7年) ★ | 5 | 京都府立高校 (R5年) ★ |
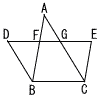 AB‖EC,AC‖DB,DE‖BCである。また,線分DEと線分AB,ACとの交点をそれぞれF,Gとすると,AF:FB=2:3であった。BC=10cmのとき,線分DEの長さを求めよ。 AB‖EC,AC‖DB,DE‖BCである。また,線分DEと線分AB,ACとの交点をそれぞれF,Gとすると,AF:FB=2:3であった。BC=10cmのとき,線分DEの長さを求めよ。 |
|||
| 2 | 帝塚山泉ヶ丘高校 (R7年) ★ | 6 | 筑波大附属駒場高校 (R5年) ★★★ |
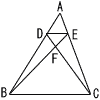 下の図のような△ABCがある。辺ACを3等分する点をD,E,辺BCの中点をFとし,AFとBD,BEの交点をそれぞれG,Hとする。BG:GDをもっとも簡単な整数の比で表しなさい。 下の図のような△ABCがある。辺ACを3等分する点をD,E,辺BCの中点をFとし,AFとBD,BEの交点をそれぞれG,Hとする。BG:GDをもっとも簡単な整数の比で表しなさい。 |
AB=16cm,BC=(8+6 点Dは辺AB上にあり,BD=(8+4 点Eは辺BC上にあり,BE=( 点Fは辺BC上にあり,CF=( 点Gは辺AC上にあり,CG=( △ABCの面積をScm2として (1) △ADGの面積を,Sを用いて表しなさい。 (2) △DEGの面積を,Sを用いて表しなさい。 (3) 線分FGの長さを求めなさい。 |
||
| 3 | 慶応義塾高校 (R7年) ★★★ | ||
 右の図のようにAD 右の図のようにAD |
|||
| 4 | 慶應義塾志木高校 (R6年) ★★★ | 7 | 大阪教育大平野校舎 (R6年) ★★★ |
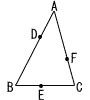 右図の△ABCにおいて,AD:DB=1:2,BE:EC=2:3,CF:FA=3:4である。△ABCの面積をSとするとき,次の図形の面積をSを用いて表せ。 右図の△ABCにおいて,AD:DB=1:2,BE:EC=2:3,CF:FA=3:4である。△ABCの面積をSとするとき,次の図形の面積をSを用いて表せ。(1) 四角形DBCF (2) 線分AEと線分DFの交点をGとするとき,△DEG |
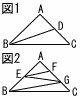 AB=AC=10cmの直角二等辺三角形ABCがある。図1は,辺AC上に点Dをとり,線分BDで△ABCの面積を二等分したものである。図2は,辺AB上に点E,辺AC上に点F,Gをとり,線分BG,GE,EFで△ABCの面積を四等分したものである。 AB=AC=10cmの直角二等辺三角形ABCがある。図1は,辺AC上に点Dをとり,線分BDで△ABCの面積を二等分したものである。図2は,辺AB上に点E,辺AC上に点F,Gをとり,線分BG,GE,EFで△ABCの面積を四等分したものである。(1) 線分BDの長さを求めなさい。 (2) 線分FGの長さを求めなさい。 |
||