| 2 相似な図形 | 月 日( ) |
| 2 相似な図形 | 月 日( ) |
| 1 | 東京工大附属科技高校 (R5年) ★★ | 5 | 青雲高校 (R4年) ★★★ |
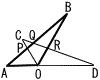 OA=1cm,OB=2cm,∠AOB=120°の△OABがある。図のように,△OABを点Oを中心として時計回りに60°だけ回転移動させたものを△OCDとする。辺ABとOCの交点をP,ABとCDの交点をQ,OBとCDの交点をRとするとき, OA=1cm,OB=2cm,∠AOB=120°の△OABがある。図のように,△OABを点Oを中心として時計回りに60°だけ回転移動させたものを△OCDとする。辺ABとOCの交点をP,ABとCDの交点をQ,OBとCDの交点をRとするとき,(1) 線分ORの長さを求めなさい。 (2) 線分AQとQBの長さの比AQ:QBをもっとも簡単な整数の比で表しなさい。 (3) 線分APとQRの長さの比AP:QRをもっとも簡単な整数の比で表しなさい。 |
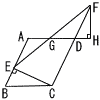
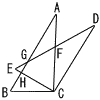 BC=2 BC=2(1) 線分CFの長さを求めよ。 (2) 線分EHの長さを求めよ。 (3) △GEHの面債を求めよ。 (4) 四角形CFGHの面積を求めよ。 |
||
| 2 | 桐光学園高校 (R6年) ★★★ | 6 | 城北高校 (R6年) ★★ |
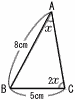 図のような△ABCにおいて,∠Cの大きさは∠Aの大きさの2倍である。このとき,辺ACの長さを求めよ。 図のような△ABCにおいて,∠Cの大きさは∠Aの大きさの2倍である。このとき,辺ACの長さを求めよ。 |
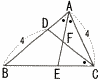 右の図のように辺AB上に点D,辺BC上に点Eをとり,AEとCDの交点をFとする。AC=BD=4,∠BAE=∠EAC=∠DCB,CF:FD=2:1であるとき,BEの長さを求めよ。 右の図のように辺AB上に点D,辺BC上に点Eをとり,AEとCDの交点をFとする。AC=BD=4,∠BAE=∠EAC=∠DCB,CF:FD=2:1であるとき,BEの長さを求めよ。 |
||
| 3 | 成蹊高校 (R6年) ★★ | 7 | 早大高等学院 (R6年) ★ |
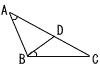 図のように,△ABCの辺AC上に,∠BAC=∠CBDとなるように点Dをとる。AB=3,BC=4,BD=2であるとき,線分ADの長さを求めよ。 図のように,△ABCの辺AC上に,∠BAC=∠CBDとなるように点Dをとる。AB=3,BC=4,BD=2であるとき,線分ADの長さを求めよ。 |
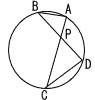 図のように,円周上に4点A,B,C,Dがある。線分ACと線分BDの交点をPとする。AB=3,BP=x,CP=x+2,CD=x+1であるとき,xの値を求めよ。 図のように,円周上に4点A,B,C,Dがある。線分ACと線分BDの交点をPとする。AB=3,BP=x,CP=x+2,CD=x+1であるとき,xの値を求めよ。 |
||
| 4 | 筑波大附属高校 (R7年) ★★ |
(2) BDの長さは, [ ] cmである。 (3) △ABCの面積は, [ ] cm2である。 |
|
 右の図のような△ABCにおいて,∠Aの内角を三等分する2直線と辺BCとの交点をそれぞれD,Eとするとき,DE=6cm,AE=CE=10cmであった。 右の図のような△ABCにおいて,∠Aの内角を三等分する2直線と辺BCとの交点をそれぞれD,Eとするとき,DE=6cm,AE=CE=10cmであった。(1) ADの長さは, [ ] cmである。 (右へつづく→) |
|||