| １ | 東京工大附属科技高校 （Ｒ５年） ★★ | ５ | 青雲高校 （Ｒ４年） ★★★ | ||||||||||||
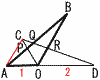 △OABを点Oを中心として時計回りに60°だけ回転移動させたものを△OCDとする。(1) 線分ORの長さを求めなさい。 【解】△AOCは正三角形 △DOR∽△DAC(相似比2:3) OR:AC＝DO:DAより,OR:1＝2:3で, OR＝  cm(2) 長さの比AQ:QBを整数の比で表しなさい。 【解】△QAC∽△QBR AQ:QB＝AC:BR=1:(2-  )＝1: ＝3:4(3) 長さの比AP:QRを整数の比で表しなさい。 【解】 △ACP∽△BOP(相似比1:2)より,AP＝  AB…ア(2)より,QR＝  CR＝(CD)＝ CD…イAB＝CDだから,アイより, AP:QR＝ :＝7:4 |
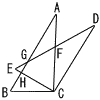 BC＝2√2cm,∠BAC＝30°∠ACB＝90°の△ABCがある。(1) 線分CFの長さを求めよ｡ 【解】△CEFは正三角形 CF＝CE＝2√2cm (2) 線分EHの長さを求めよ。 【解】△BCHは,30,60,90度 CH＝  BC＝√6より, EH＝(2√2−√6)cm(3) △GEHの面債を求めよ｡ 【解】△EGH∽△BCH GH＝√3(2√2−√6)＝√6(2−√3)より, △GEH＝  ×√2(2−√3)×√6(2−√3)＝(7√3−12)cm2 (4) 四角形CFGHの面積を求めよ。 【解】△CEF−△GEH ×2√2×(2√2×)−(7√3−12)＝(12−5√3)cm2 |
||||||||||||||
| ２ | 桐光学園高校 （Ｒ６年） ★★★ | ６ | 城北高校 （Ｒ６年） ★★ | ||||||||||||
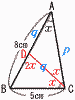 ,辺ACの長さを求めよ。【解】∠Cの二等分線CDを引くと, 2角相等より,△ABC∽△CBD p＝AC,q＝AD＝CDとすると, AB:CB＝ＡC:ＣＤより,8:5＝p:q…ア CA:CB＝AD:BDより,p:5＝q:(8−q)…イ アイより,p＝AC＝39/5 |
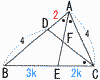 BEの長さを求めよ。【解】 △ACDで,AC:AD＝2:1より,AD＝2 △ABCで,BE:CE＝6:4＝3:2 ここで,BE＝3k,CE＝2kとする △ABE∽△CBDより,6:5k＝3k:4 15k2＝24より,k＝  √10で, BE＝3×√10＝ √10 |
||||||||||||||
| ３ | 成蹊高校 （Ｒ６年） ★★ | ７ | 早大高等学院 （Ｒ６年） ★ | ||||||||||||
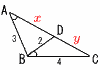 図のように,△ABCの辺AC上に,∠BAC＝∠CBDとなるように点Dをとる。AB＝3,BC＝4,BD＝2であるとき,線分ADの長さを求めよ。【解】2角相等より,△ABC∽△BDC
 |
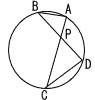 図のように,円周上に4点A,B,C,Dがある。線分ACと線分BDの交点をPとする。AB＝3,BP＝x,CP ＝x＋2,CD＝x＋1であるとき,xの値を求めよ。【解】2角相等より,△ABP∽△DCP 3:(x＋1)＝x:(x＋2)を解いて, x＝1＋√7 |
||||||||||||||
| ４ | 筑波大附属高校 （Ｒ７年） ★★  |
(2) BDの長さは, [ ] ｃｍである。 【解】BD＝xとすると,AB＝x＋6 △ABD∽△CBAより,(x＋6):x＝(x＋16):(x＋6)で,x＝BD＝9cm 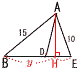 (3) △ABCの面積は, [ ] cm2である。【解】垂線AHをおろし,BH＝yとすると,△ABEで, AH2＝152−y2＝102−(15−y)2より,y＝35/3 AH2＝152−(35/3)2＝800/9で,AH＝   △ABC＝  ×25×()＝(250/3) cm2 |
|||||||||||||
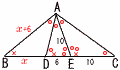 右の図のような△ABCにおいて,∠Aの内角を三等分する2直線と辺BCとの交点をそれぞれD,Eとするとき,DE＝6cm,AE＝CE＝10cmであった。(1) ADの長さは, [ ] ｃｍである。 【解】△ADE∽△CDA(2角相等)より,AD:6＝16:ADで, AD＝4  cm(右へつづく→) |
|||||||||||||||
