 関数 |
２１ 放物線と平行線 | 月 日（ ） |
| 関数 |
２１ 放物線と平行線 | 月 日（ ） |
| １ | 東京工大附属科技高校 （Ｒ５年） ★★ | ４ | 桐光学園高校 （Ｒ５年） ★★ |
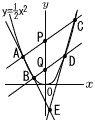 図のように,関数,y＝ x2のグラフ上にx座標が負である点A,Bをとり,x座標が正である点C,Dをとる。直線ACと直線BDの傾きはともに1であり,AC,BDとy軸との交点をそれぞれP,Qとすると,AP:PC＝2:3,BQ:QD＝1:2である。また,直線ABとCDの交点をEとするとき，(1) 点Aの座標を求めなさい。 (2) 直線BDの式を求めなさい。 (3) 四角形ABDCの面積をS,△BDEの面積をTとするとき,S:Tをもっとも簡単な比で表しなさい。 |
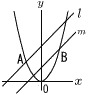 図のように,放物線y＝x2…①,直線l：y＝x＋4…②,および直線l と平行な直線mがある。直線l と放物線①の交点のうちx座標が小さい方をA,直線mと放物線①の交点のうちx座標が大きい方をBとする。点Bのx座標が3であるとき,(1) 点Aの座標を求めよ。 (2) 直線mの式を求めよ。 (3) 点Aで直線l に接する円が,直線m上の2点B,Pを通るとき,点Pの座標を求めよ。 |
||
| ２ | 中央大附属横浜高校 （Ｒ７年） ★★ | ５ | 灘 高校 （Ｒ５年） ★★ |
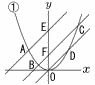 図において,曲線①は関数y＝ax2のグラフであり,点A,B,C,Dはこの曲線上にある。 Aの座標は（－2,2）であり,B,C,Dのx座標はそれぞれ－1,3,2である。また,点Eはy軸上の点,点Fはy軸と直線BCの交点であり,3 つの直線AE,BC,OD は平行である。 (1) aの値を求めなさい。 (2) 直線BCの式をy＝mx＋nの形で答えなさい。 (3) 三角形CFDの面積は三角形BFAの面積の何倍であるか求めなさい。 |
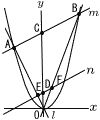 aは2より小さい正の数である。放物線y＝ax2…①と直線l :y＝－2xがある。①とl の交点のうち,原点O(0,0)でない方をAとする。また,Aを通り傾きがである直線をmとし,①とmの交点のうちAでない方をBとする。(1) A,Bの座標をaを用いて表すと,A( , ) B( , )である。 (2) mとy軸の交点をCとする。点D(0,a)を通り直線mに平行な直線をnとする。l とnとの交点をEとし,nと直線OBとの交点をFとする。 (a) △ODFの面積をaを用いて表せ。 (b) △ODFの面積と四角ACDEの面積が等しいようなaの値を求めよ。 |
||
| ３ | 近畿大附属高校 （Ｒ６年） ★★★ | ６ | 同志社高校 （Ｒ６年） ★★★ |
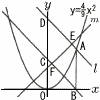 a＞0とする。図のように放物線y＝ x2に点Ａ(a,4)がある。Aからx軸にひいた垂線とx軸との交点をBとし,点(0,3)をCとする。Ａを通り直線BCに平行な直線をl とし,l とy軸との交点をDとする。点(0,2)を通り,四角形ABCDの面積を二等分する直線をmとする。mとl との交点をE,mと直線BCとの交点をFとする。(1) aの値を求めよ。 (2) 直線l の式を求めよ。 (3) 直線mの式を求めよ。 (4) 四角形ABFEを線分ABを軸に一回転させてできる立体の体積を求めよ。ただし,円周率をπとする。 |
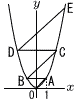 図のように放物線y＝x2上に点A,B,C,D,Eをとると,線分AB,CDがともにx軸と平行で,3本の線分OA,BCDEがそれぞれ平行になった。点Ａのx座標を１とするとき,(1) 直線BCの方程式と点Eの座標を求めよ。 (2) △ABCと△CDEの面積比を最も簡単な整数の比で表せ。 (3) △OABと六角形OACEDBの面積比を最も簡単な整数の比で表せ。 (4) 点Eを通り六角形OACEDBの面積を二等分する直線の方程式を求めよ。 |
||
