 関数 |
１９ 二つの放物線２ | 月 日（ ） |
| 関数 |
１９ 二つの放物線２ | 月 日（ ） |
| １ | 法政大高校 （Ｒ５年） ★★★ | ４ | 東大寺学園高校 （Ｒ５年） ★★ |
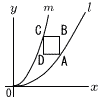 右の図の曲線l は放物線y＝ x2のx≧0の部分である。曲線mは放物線y＝ax2のx≧0の部分である。また,四角形ABCDは１辺3の正方形で,頂点Aは曲線l 上に,頂点Cは曲線m上にあり,辺ABはy軸に平行である。ただし,a＞とし,頂点Aのx座標は3よりも大きいものとする。(1) 頂点Aのx座標が4のとき,直線ACの式を求めなさい。 (2) a＝2のとき,頂点Aのx座標を求めなさい。 |
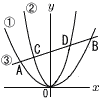 0＜a＜bとする。原点をOとするxy平面上に2つの放物線y＝a2x2…①,y＝b2x2…②と1つの直線y＝ax＋6…③があり,①と③が相異なる2点A,Bで交わり,②と③が相異なる2点C,Dで交わっている。ただし,Aのx座標はBのx座標より小さく,Cのx座標はDのx座標より小さいものとする。(1) A,Bの座標をそれぞれaを用いて表せ。 (2) 三角形OABの面積が30のとき,aの値を求めよ。 (3) (2)のとき,三角形OBDの面積が6であるとする。このとき,三角形OCAの面積を求めよ。 |
||
| ２ | 日大第三高校 （Ｒ７年） ★★★ | ５ | 西大和学園高校 （Ｒ７年） ★★★ |
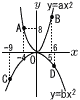 右の図のように,関数y＝ax2のグラフ上に2点A,Bがあり,点Ａの座標は(－4,8),点Bのx座標は5である。また,関数y＝bx2のグラフ上に2点C,Dがあり,x座標はそれぞれ－9,6である。ただし,グラフの１目盛りを１cmとする。(1) aの値を求めなさい。 (2) 直線ABの式を求めなさい。 (3) y＝bx2のxの値が－9から6まで変化するときの変化の割合を,bを用いて表しなさい。 (4) AB∥CDのとき,四角形ACDBの面積を求めなさい。 |
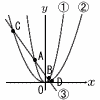 aを正の定数とする。図において曲線C1,曲線 C2,直線l はそれぞれ,放物線y＝x2…①,放物線 y＝ax2…②,直線y＝－2x＋3…③のグラフである。C1とl との交点をx座標が小さ い順に点A,Bとし,C2とl との交点をx座標が小さい順に点C,Dとする。 △OABと△OCDの面積の比が1:7であるとき,(1) 三角形OABの面積を求めよ。 (2) 定数aの値を求めよ。 (3) 直線m：y＝－2x＋5とC1との交点をx座標が小さい順に点P,Qとするとき,五角形OAPQBの面積を求めよ。 |
||
| ３ | 日本大第二高校 （Ｒ６年） ★★★ | ６ | 明治大付属明治高校 （Ｒ６年） ★★★ |
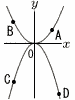 図のように放物線y＝ x2と放物線y＝－x2について,2点A,Bは放物線y＝x2上にあり,2点C,Dは放物線y＝－x2上にあるものとする。点A,Dのx座標は正であり,点B,Cのx座標は等しく,負である。また,点Ｂのy座標は点Ａのy座標より１大きく,点Ｄのy座標は点Cのy座標より１小さいものとする。(1) 点Ａのx座標が2のとき点Ｄの座標を求めよ。 (2) 点Ａのx座標をtとする。 BCの長さが50のとき,tの値を求めよ。 (3) 点Ａのx座標と点Dのx座標の差が2になるとき,点Ａの座標を求めよ。 |
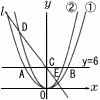 右の図のように2つの放物線y＝ x2…①,y＝ax2…②がある。放物線①と直線y＝6の2つの交点のうち,x座標が小さい方を点Ａ,もう1つの交点を点Ｂとする。また,点C(0,6)を通り,傾きが負である直線をl とし,放物線②と直線l の2つの交点のうち,x座標が小さい方を点D,もう1つの交点を点Eとする。△AOB＝△DOEであるとき。ただし,,a＞とする。(1) △AOBの面積を求めよ。 (2) CD:CE＝3:1のとき,aの値を求めよ。 (3) (2)のとき,△DPEの面積が,△DOEの面積の  倍となるように点Pを放物線①上にとる。このとき,点Pのx座標をすべて求めよ。 |
||
