２　関数 １９　二つの放物線２　（略解）
１ 法政大高校　（Ｒ５年）　★ ４ 東大寺学園高校　（Ｒ５年）　★★★
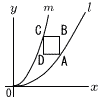　右の図の曲線l は放物線y＝x2のx≧0の部分である。曲線mは放物線y＝ax2のx≧0の部分である。また,四角形ABCDは１辺3の正方形で,頂点Aは曲線l 上に,頂点Cは曲線m上にあり,辺ABはy軸に平行である。ただし,a＞とし,頂点Aのx座標は3よりも大きいものとする。
(1) 頂点Aのx座標が4のとき,直線ACの式を求めなさい。
【解】A(4,8)より,C(1,11)
y＝ 8－11 (x－1)＋11で, y＝－x＋12
4－1
(2) a＝2のとき,頂点Aのx座標を求めなさい。
【解】A(t,t2)とすると,C(t－3,t2＋3)
これをmに代入して,t2＋3＝2(t－3)2
　t2－8t＋10＝0　t＞3だから, t＝4＋√6		 　放物線y＝a2x2…①,y＝b2x2…②と直線y＝ax＋6…③がある。
(1) A,Bの座標をそれぞれaを用いて表せ。
【解】A,Bは①＝③より,a2x2＝ax＋6
(ax＋2)(ax－3)＝0で, A(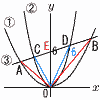－,4) B(,9)
(2) △OAB=30のとき,aの値
【解】△OAB＝OE×(BとAのx座標差)
×6×(＋)＝30で, a＝
(3) △OBD＝6のとき,△OCAの面積
【解】A(－4,4) B(6,9)　D(t,b2t2)とすると,
△OBD＝×6×(6－t)＝6で,t＝4
これを②③に代入して,16b2＝×4＋6で,b2＝
Cは②＝③より,x2＝x＋6で,C(－3,)
　△OCA＝×6×(4－3)＝3
２ 日大第三高校　（Ｒ７年）　★★★ ５ 西大和学園高校　（Ｒ７年）　★★★
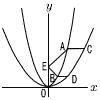(1) aの値を求めなさい。
【解】A(－4,8)を代入して,(－4)2a＝8より, a＝
(2) 直線ABの式を求めなさい。
【解】B(5,25/2)　ABの傾き＝ 25/2-8 ＝ 1
5－(－4) 2
　y＝(x＋4)＋8より, y＝x＋10 …ア
(3) y＝bx2のxの値が－9から6まで変化するときの変化の割合を,bを用いて表しなさい。
【解】変化の割合＝ 62ｂ－(－9)2ｂ ＝ 36ｂ－81ｂ ＝－3ｂ
6－(－9) 15
(4) AB∥CDのとき,四角形ACDBの面積を求めなさい。
【解】ABとCDの傾きは等しいから,＝－3ｂより, ｂ＝－
C(－9,－27/2)　D(6,－6) となって,CDはｙ＝ｘ－9 …イ
アとイのｙ座標差＝10－(－9)＝19…ウ
△ACD＋△ABD＝×19×(CとDのｘ座標差)＋×19×(AとBのｘ座標差)
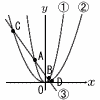　＝×19×(6＋9)＋×19×(5＋4)＝228cm2		 　 三角形OABと三角形OCDの面積の比が1：7であるとき,

(1) 三角形OABの面積を求めよ。
【解】A(－3,9) B(1,1) ③の切片は3
×3×（AとBのx座標差)＝×3×（1＋3)＝6
(2) 定数aの値を求めよ。
【解】
ax2＝－2x＋3より,CとDのx座標差は
△OAB：△OCD＝(AとBのx座標差)：(CとDのx座標差)＝1:√7
　(CとDのx座標差)＝＝4√7より, a＝
(3) 直線m：y＝－2x＋5とC1との交点をx座標が小さい順に点P,Qとするとき,五角形OAPQBの面積を求めよ。
【解】QとPのx座標は－1±√6　ABとPQのy座標差は2
△PAB＋△PQB＋△OAB
　＝×2×(ABのx座標差)＋×2×(PQのx座標差)＋6
　＝(1＋3)＋(－1＋√6＋1＋√6)＋6＝10＋2√6
３ 日本大第二高校　（Ｒ６年）　★★★ ６ 明治大付属明治高校　（Ｒ６年）　★★★
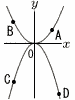　放物線y＝x2…アと放物線y＝－x2…イ
(1) 点Ａのx座標が2のとき点Ｄの座標を求めよ。
【解】A(2,1),B(－2√2,2)，C(－2√2,－8)
イにy＝－9を代入して, D(3,－9)
（2）点Ａのx座標をtとする。 BCの長さが50のとき,tの値を求めよ。
【解】B(s,t2＋1)としてアに代入すると,t2＋1＝s2…ウ
C(s,t2＋1－50)で,イに代入すると,t2－49＝－s2…エ
ウエを連立させて解いて, t＝6
（3）点Ａの座標を求めよ。
【解】点Ａのx座標をtとすると,D(t＋2,－(t＋2)2)
C(s,－(t＋2)2＋1)で,イに代入すると,－(t＋2)2＋1＝－s2…オ
ウオを連立させて解いて,t＝より, A(1/4,1/64)		 　2つの放物線y＝x2…①,y＝ax2…②がある。
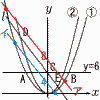(1) △AOBの面積を求めよ。
【解】A(－6,6),B(6,6)
△AOB＝×12×6＝36
(2) CD:CE＝3:1のとき,aの値を求めよ。
【解】E(e,ae2)とすると,D(－3e,9ae2)
△DOE＝×6(e＋3e)＝36より,E(3,9a),D(－9,81a)
l はy＝－6ax＋6で,Ｅを代入して,9a＝－18a＋6より, a＝
(3) 点Pのx座標をすべて求めよ。
【解】(右上図参照)　l に平行な2直線との交点
・①とアの交点は,x2＝－x＋8で, x＝－12,4
・①とイの交点は,x2＝－x＋4で, x＝－4±2√10

［TOP］　［問題に戻る］　　★　中　　★★　やや難　　★★★　難