| 1 |
四天王寺高校 (R5年) ★ |
6 |
大阪府立高校C (R5年) ★★ |
\(\sqrt{847n}\)が整数となる自然数nのうち,最も小さいものはn=( )です。このとき,\(\sqrt{847n}\)=( )です。
|
nを自然数とする。n≦\(\sqrt{x}\)≦n+1を満たす自然数xの個数が100であるときのnの値を求めなさい。
|
| 2 |
桃山学院高校 (R5年) ★ |
7 |
桐朋高校 (R5年) ★ |
\(\sqrt{\frac{2023}{n}}\)が自然数となるような自然数nをすべて求めなさい。
|
1+\(\sqrt3\)の整数部分をa,小数部分をbとするとき,ab+b2の値を求めよ。
|
| 3 |
京華高校 (R5年) ★★ |
8 |
早大高等学院 (R7年) ★★★ |
\(\sqrt{\frac{20a}{3}}\)が2桁の自然数の中で最も大きくなるよ うな自然数aの値を求めよ。
|
\(\sqrt7\)×\(\sqrt{17}\)の整数部分をA, B=282−(\(\frac{35}{3}\))2とするとき,
(1) Aの値を求めよ。
| (2) |
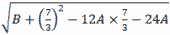 |
の値を求めよ。 |
|
| 4 |
都立産技高専 (R7年) ★★ |
\(\sqrt{5n+225}\) が自然数となるような最も小さい自然数nの値を求めよ。
|
| 5 |
中央大杉並高校(R6年) ★ |
9 |
明治大付属中野高校(R6年) ★★★ |
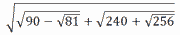 |
を計算しなさい。 |
|
5−\(\sqrt7\)の整数部分をa,小数部分をbとするとき,
| 3a2−5ab+2b2 |
の値を求めなさい。 |
| a2−ab |
|