| 1 |
大阪教育大平野校舎 (R5年) ★ |
6 |
明治学院高校 (R5年) ★ |
\(\small\sqrt{(\pi-3)^2}+\sqrt{(3-\pi)^2}\)の値を, πを用いて簡 単に表しなさい。πは円周率を表すものとする。
|
\(\sqrt{\frac{300}{n}}\)が整数となるような自然数nはいくつあるか。
|
| 2 |
桃山学院高校 (R7年) ★ |
7 |
明治大付属中野高校 (R5年) ★★ |
\(\small\sqrt{360-24n}\)が自然数となるような自然数nの値を求めなさい。
|
\(\sqrt{2233-33n}\)が整数となるような自然数nの値をすべて求めなさい。
|
| 3 |
芝浦工大附属高校 (R7年) ★★ |
8 |
東海高校 (R5年) ★★ |
nは自然数とする。\(\small\sqrt{2025+n}\)の値が自然数となる最小のnの値を求めなさい。
|
\(a=2(\sqrt{13}-2)\)の整数部分をb,小数部分をcとする。このとき, (a+3b+1)(c+1)の値は( )である。
|
| 4 |
巣鴨高校 (R5年) ★★★ |
9 |
洛南高校 (R5年) ★★★ |
\(\sqrt{n^2+104}\)が自然数となるような自然数nを すべて求めなさい。
|
\(\sqrt{2023n}\)が整数となるような4桁の正の整数nのうち,最小のものを求めなさい。
|
| 5 |
慶應義塾高校(R6年) ★★ |
10 |
渋谷教育学園幕張高校(R6年) ★★ |
\(\frac{14+3\sqrt{7}}{\sqrt{7}}\)の小数部分をaとするとき, \(a+\frac{1}{a}\)の値は( )である。
|
次の計算をしなさい。
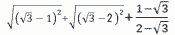
|