 データの活用 |
１３ 数列２ | 月 日（ ） |
| データの活用 |
１３ 数列２ | 月 日（ ） |
| １ | 聖徳学園高校 （Ｒ７年） ★ | ５ | 上宮高校 （Ｒ７年） ★★ | ||||||||||||||||||||||||
| 32024の一の位の数字は[ ]である。 |
 同じ大きさの正方形のタイルを白,黒の順に並べ,右のような図形を作っていきます。
(1) 8番目の図形について,白のタイルの枚数を求めなさい。 (2) 10番目の図形について,黒のタイルの枚数を求めなさい。 (3) 16番目の図形について,タイルの合計枚数を求めなさい。 (4) 100番目の図形について,白のタイルと黒のタイルの枚数の差を求めなさい。ただし,差は正の数で答えなさい。 |
||||||||||||||||||||||||||
| ２ | 明治学院東村山高校 （Ｒ４年） ★★ | ||||||||||||||||||||||||||
| 以下のように規則的に数が並んでいるとき, 2, 4, 4, 6, 6, 6, 8, 8, 8, 8, 10, 10, 10, 10, 10, 12, … (1) 21番目までのすべての数の和を求めなさい。 (2) 50番目の数を求めなさい。 (3) 100を初めて超えるのは,何番目の数か求めなさい。 |
|||||||||||||||||||||||||||
| ３ | 京都府立鳥羽高校 （Ｒ７年） ★★ | ６ | 近畿大附属豊岡高校 （Ｒ５年） ★ | ||||||||||||||||||||||||
| 4つの整数2,6,7,8をある規則にしたがって,次のように左から並べた。 ７,６,２,７,６,８,８,７,６,２,7,６,８,８,７,６,２,７,６,８,８,… (1) 左から数えて25番目の数を求めよ。 (2) 左から数えて100番目の数を求めよ。 (3) 2025回目の8は左から数えて何番目の数か。例えば,4回目の8は左から数えて14番目の数である。 |
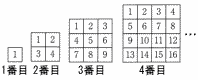 自然数が書かれた正方形のカードを図のように縦と横が同じ枚数となるように,左上から小さい数順に並ぺる。(1) nは2以上の自然数とする。n番目で左下の隅にあるカードに書かれた数をnの式で表しなさい。 (2) n番目で,四隅の4つの数の和が394になるとき,nの値を求めなさい。 |
||||||||||||||||||||||||||
| ４ | 常盤高校 （Ｒ６年） ★ | ７ | 宇都宮短大附属高校 （Ｒ６年） ★★ | ||||||||||||||||||||||||
 正方形の白板と黒板を図のように規則的に増やしていく。(1) 6段のとき,白板は[ ]枚である。 (2) n段のとき,白板は[ ]枚である。ただし,nを使った最も簡単な式で表せ。 (3) 白板がちょうど26枚のとき,黒板は[ ]枚であ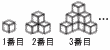る。 |
 図のように,同じ大ききの立方体のブロックをある規則にしたがってすき間なくつなぎ合わせて立体をつくる。(1) 立体をつくるときに図の角度からは見えないブロックの個数を考える｡例えば,3番目の立体では見えないブロックは2個である。4番目の立体において,見えないブロックの個数を求めよ。 (2) n番目の立体において,見えないブロックの個数をnを用いて表せ。 (3) 4番目の立体に使われているブロックの個数を求めよ。 (4) n番目の立体に使われているプロックの個数をnを用いて表せ。 (5) ブロックが全部で2024個あるとき,それらを使ってつくりあげることができる最も大きい立体は[A ]番目の立体であり,このときプロックは[B ]個あまる。 |
||||||||||||||||||||||||||
