データの活用

１３　数列２　（略解）

１	聖徳学園高校　（Ｒ７年）　★	５	上宮高校　（Ｒ７年）　★★★
32024の一の位の数字は[　　]である。 　 【解】3の累乗の一位の数は, 3,9,7,1,…(4数ごとに繰り返す) 2024÷4＝506と,割り切れるから,くり返し最後の数で, 1		同じ大きさの正方形のタイルを白,黒の順に並べ,右のような図形を作っていきます。 ﾀｲﾙ 2番目 4番目 6番目 … 2k番目 白 1 4 9 … k2 黒 2 6 12 … k2＋k 計 3 10 21 … 2k2＋k 　表は,白と黒のタイルを並べてできた図形の,2色のタイルの枚数をまとめたものです。 (1) 8番目の図形について,白のタイルの枚数を求めなさい。 【解】偶数(2k)番目は,白k2枚, 黒(k2＋k)枚 k＝4より,42＝16枚 (2) 10番目の図形について,黒のタイルの枚数を求めなさい。 【解】 k＝5より,52＋5＝30枚 (3) 16番目の図形について,タイルの合計枚数を求めなさい。 【解】 k＝8より,2×82＋8＝136枚 (4) 100番目の図形について,白のタイルと黒のタイルの枚数の差を求めなさい。ただし,差は正の数で答えなさい。 【解】 k＝50より, 黒−白＝(502＋50)−502＝50枚
２	明治学院東村山高校　（Ｒ４年）　★★
以下のように規則的に数が並んでいるとき, 2,|4, 4,|6, 6, 6,|8, 8, 8, 8,|10, 10, 10, 10, 10,|12, … (1) 21番目までのすべての数の和 【解】1＋2＋…＋6＝21で,6群の最後の項 和＝2＋4×2＋6×3＋…＋12×6 　＝2＋8＋18＋32＋50＋72＝182 (2) 50番目の数 【解】1＋2＋…＋9＝45で,10群　　10×2＝20 (3) 100を初めて超えるのは,何番目の数か 【解】100が50個並ぶのは50群 1＋2＋…＋50＝×50×51＝1275番目 1275＋1＝1276番目
３	京都府立鳥羽高校　（Ｒ７年）　★★	６	近畿大附属豊岡高校　（Ｒ５年）　★
4つの整数2,6,7,8をある規則にしたがって,次のように左から並べた。 　７,６,２,７,６,８,８|７,６,２,7,６,８,８|７,６,２,７,６,８,８| … (1) 左から数えて25番目の数を求めよ。 【解】7項ごとに繰り返している 25÷7＝3余り4だから,4群の4項目で, 7 (2) 左から数えて100番目の数を求めよ。 【解】100÷7＝14余り2だから,15群の2項目で, 6 (3) 2025回目の8は左から数えて何番目の数か。例えば,4回目の8は左から数えて14番目の数である。 【解】1群に8は2個あるから,1013群の6項目 7×1012＋6＝7090番目		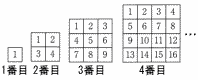正方形のカードを図のように並ぺる。 (1) nは2以上の自然数とする。n番目で左下の隅にあるカードに書かれた数をnの式で表しなさい。 【解】右下の数より(n−1)小さいから, 　n2−(n−1)＝n2−n＋1 (2) n番目で,四隅の4つの数の和が394になるとき,nの値 【解】左上＝1, 右上＝n, 左下＝n2−n＋1, 右下＝n2 　1＋n＋(n2−n＋1)＋n2＝394 　2n2＋2＝394で, n＝14
４	常盤高校　（Ｒ６年）　★	７	宇都宮短大附属高校　（Ｒ６年）　★★
正方形の白板と黒板を図のように規則的に増やしていく。 (1) 6段のとき,白板は[　　]枚である。 【解】白は3枚ずつ増えて, 5,8,11,14,17 (2) n段のとき,白板は[　　]枚である。ただし,nを使った最も簡単な式で表せ。 【解】5＋3(n−2)＝3n−1 (3) 白板がちょうど26枚のとき,黒板は[　　]枚である。 【解】3n−1＝26より,n＝9段 よって, (9−1)2＝64		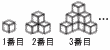立方体をつなぎ合わせて立体をつくる。 (1) 4番目の立体で,見えないブロックの個数 【解】奥の縦で, 3個 (2) n番目の立体で,見えないブロックの個数をnを用いて表せ。 【解】奥の縦はn個だから, n−1個 (3) 4番目の立体に使われているブロックの個数を求めよ。 【解】1＋3＋5＋7＝16個 (4) n番目の立体のプロックの個数をnを用いて表せ。 【解】1,4,9,16,…, n2個 (5) ブロックが2024個あるとき,最も大きい立体は[A　]番目の立体であり,このときプロックは[B　]個あまる。 【解】n2＜2024より, n＝44番目 2024−442＝88個

［TOP］　［問題に戻る］　　★　中　　★★　やや難　　★★★　難