| ‚P‚UЃ@•ъ•Ёђь‚Ж’јђь‚R | Ѓ@Ѓ@Ѓ@ЊЋЃ@Ѓ@Ѓ@“ъЃiЃ@Ѓ@Ѓj |
| ‚P‚UЃ@•ъ•Ёђь‚Ж’јђь‚R | Ѓ@Ѓ@Ѓ@ЊЋЃ@Ѓ@Ѓ@“ъЃiЃ@Ѓ@Ѓj |
| ‚P | ‘Ѓ€о“c‘еЌ‚“™Љw‰@Ѓ@Ѓi‚q‚T”NЃjЃ@ЃљЃљЃљ | ‚S | “ъ–{‘е‘жЋOЌ‚ЌZЃ@Ѓi‚q‚T”NЃjЃ@ЃљЃљ |
| Ѓ@a‚рђі‚М’иђ”‚Ж‚·‚йЃB•ъ•ЁђьyЃЃx2‚Ж’јђьyЃЃaxЃ{2a‚Ж‚МЊр“_‚р A,B‚Ж‚µ,•ъ•ЁђьyЃЃx2‚Ж’јђьyЃЃ(3Ѓг2Ѓ|4)xЃ{6Ѓг2Ѓ|8‚Ж‚МЊр“_‚рC,D‚Ж‚·‚йЃB‚Ѕ‚ѕ‚µ,“_A‚МxЌА•W‚НЃ|1‚Е‚ ‚и,“_C‚МxЌА•W‚Н“_D‚МxЌА•W‚ж‚и‚аЏ¬‚і‚ўЃB‚Ь‚Ѕ,’јђьyЃЃaxЃ{2a‚ЖxЋІ‚Ж‚МЊр“_‚рE‚Ж‚·‚йЃB (1) a‚М’l‚р‹Ѓ‚Я‚жЃB (2) EA/EB ‚М’l‚р‹Ѓ‚Я‚жЃB (3) “_C‚МxЌА•W‚р‹Ѓ‚Я‚жЃB (4) 4“_A,B,C,D‚р’ё“_‚Ж‚·‚йЋlЉpЊ`‚М–КђП‚р‹Ѓ‚Я‚жЃB Ѓ@ |
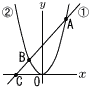 Ѓ@‰E‚Мђ}‚̂悤‚Й,’јђь‡@‚МѓOѓ‰ѓt‚Ж•ъ•Ёђь‡A‚МѓOѓ‰ѓt‚Є2“_A,B‚ЕЊр‚н‚Б‚Д‚ў‚йЃB‚і‚з‚Й,‡@‚НxЋІ‚Ж“_C‚ЕЊр‚н‚Б‚Д‚ў‚йЃB‚`(4,8),C(Ѓ|4,0),“_B‚МxЌА•W‚рЃ|2‚Ж‚·‚йЃB‚Ѕ‚ѕ‚µ,ЌА•W‚М‚P–Ъђ·‚и‚р1cm‚Ж‚·‚йЃB Ѓ@‰E‚Мђ}‚̂悤‚Й,’јђь‡@‚МѓOѓ‰ѓt‚Ж•ъ•Ёђь‡A‚МѓOѓ‰ѓt‚Є2“_A,B‚ЕЊр‚н‚Б‚Д‚ў‚йЃB‚і‚з‚Й,‡@‚НxЋІ‚Ж“_C‚ЕЊр‚н‚Б‚Д‚ў‚йЃB‚`(4,8),C(Ѓ|4,0),“_B‚МxЌА•W‚рЃ|2‚Ж‚·‚йЃB‚Ѕ‚ѕ‚µ,ЌА•W‚М‚P–Ъђ·‚и‚р1cm‚Ж‚·‚йЃB(1) “_B‚МЌА•W‚р‹Ѓ‚Я‚И‚і‚ўЃC (2) “_B‚ЖЊґ“_O‚Й‚В‚ў‚Д‘ОЏМ‚И“_‚рD‚Ж‚·‚й‚Ж‚«,ЃўADB‚М–КђП‚р‹Ѓ‚Я‚И‚і‚ўЃB (3) “_B‚©‚з’јђьAD‚Й€ш‚ў‚Ѕђ‚ђь‚М’·‚і‚р‹Ѓ‚Я‚И‚і‚ўЃB Ѓ@Ѓ@Ѓ@ |
||
| ‚Q | €¤ЊхЌ‚ЌZЃ@ЃiR‚U”NЃjЃ@ЃљЃљЃљ | ‚T | ’†‰›‘е•Ќ‘®Ќ‚ЌZЃ@ЃiR‚U”NЃjЃ@ЃљЃљЃљ |
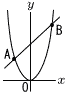 Ѓ@‰E‚Мђ}‚̂悤‚Й•ъ•ЁђьyЃЃx2‚Ж’јђьyЃЃxЃ{6‚Є‚ ‚и,‚»‚МЊр“_‚рxЌА•W‚ЄЏ¬‚і‚ўЏ‡‚Й‚`,‚a‚Ж‚·‚йЃB Ѓ@‰E‚Мђ}‚̂悤‚Й•ъ•ЁђьyЃЃx2‚Ж’јђьyЃЃxЃ{6‚Є‚ ‚и,‚»‚МЊр“_‚рxЌА•W‚ЄЏ¬‚і‚ўЏ‡‚Й‚`,‚a‚Ж‚·‚йЃB(1) “_‚`,‚a‚МЌА•W‚р‹Ѓ‚Я‚жЃB“љ‚М‚Э‚Е‚ж‚ўЃB (2) ’јђьyЃЃxЃ{6‚ЙЉЦ‚µ‚Д“_C(3,a)‚Ж‘ОЏМ‚И“_‚c‚Є•ъ•ЁђьЏг‚Й‚ ‚й‚Ж‚«,a‚М’l‚Ж“_‚c‚МЌА•W‚р‹Ѓ‚Я‚жЃB‚Ѕ‚ѕ‚µ,aЃ‚9‚Ж‚·‚йЃB (3) “_‚c‚р’К‚и,ЋlЉpЊ`‚`‚b‚a‚c‚М–КђП‚р‚Q“™•Є‚·‚й’јђь‚МЋ®‚р‹Ѓ‚Я‚жЃB Ѓ@ |
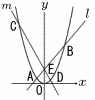 Ѓ@ђ}‚̂悤‚Й,ЉЦђ”yЃЃx2‚МѓOѓ‰ѓt‚Ж’јђьl‚МЊр“_‚р‚`,‚a,ЉЦђ”yЃЃx2‚МѓOѓ‰ѓt‚Ж’јђьm‚МЊр“_‚рC,D,’јђьl,m‚МЊр“_‚рE(0,2)‚Ж‚·‚йЃBAE:EBЃЃ1:3‚М‚Ж‚«, Ѓ@ђ}‚̂悤‚Й,ЉЦђ”yЃЃx2‚МѓOѓ‰ѓt‚Ж’јђьl‚МЊр“_‚р‚`,‚a,ЉЦђ”yЃЃx2‚МѓOѓ‰ѓt‚Ж’јђьm‚МЊр“_‚рC,D,’јђьl,m‚МЊр“_‚рE(0,2)‚Ж‚·‚йЃBAE:EBЃЃ1:3‚М‚Ж‚«,(1) ’јђьl‚МЋ®‚р‹Ѓ‚Я‚И‚і‚ўЃB (2)Ѓў‚`‚d‚b‚ЖЃў‚c‚d‚a‚М–КђП”д‚Є2:1‚М‚Ж‚«, (ѓA) “_‚c‚МxЌА•W‚р‹Ѓ‚Я‚И‚і‚ўЃB (ѓC) ’јђьm‚МЋ®‚р‹Ѓ‚Я‚И‚і‚ўЃB Ѓ@Ѓ@ |
||
| ‚R | —§‹іђVЌАЌ‚ЌZЃ@ЃiR‚V”NЃjЃ@ЃљЃљЃљ | 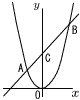 (3) “_C‚МyЌА•W‚р,a‚р—p‚ў‚Д•\‚µ‚И‚і‚ўЃB (3) “_C‚МyЌА•W‚р,a‚р—p‚ў‚Д•\‚µ‚И‚і‚ўЃB(4) ЃўOAB‚М–КђП‚Є Ѓ@ |
|
| Ѓ@ЉЦђ”yЃЃx2‚МѓOѓ‰ѓtЏг‚Й2“_A,B‚Є‚ ‚и,“_A‚МxЌА•W‚Нa,“_B‚МxЌА•W‚Н3‚Е‚·ЃB ‚Ь‚Ѕ,’јђьAB‚ЖyЋІ‚МЊр“_‚рC‚Ж‚µ‚Ь‚·ЃB‚Ѕ‚ѕ‚µ,aЃѓ0‚Ж‚µ‚Ь‚·ЃB (1) aЃЃЃ|2‚М‚Ж‚«,“_C‚МyЌА•W‚р‹Ѓ‚Я‚И‚і‚ўЃB (2) ЃўOBC‚М–КђП‚ЄЃўOAC‚М–КђП‚М2”{‚Й‚И‚й‚Ж‚«,“_C‚МyЌА•W‚р‹Ѓ‚Я‚И‚і‚ўЃB Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓi‰E‚ւ‚ÂЃЁЃj |
|||
ЃmTOPЃnЃmBACKЃnЃmNEXTЃnЃm‰р“љЃnЃ@Ѓ@Ѓљ’† ЃљЃљ‚в‚в“п ЃљЃљЃљ“пЃ@![]() €уЌь—p
€уЌь—p