| �P�U�@�������ƒ����R�@�i�����j | ||
| �P�U�@�������ƒ����R�@�i�����j | ||
| �P | ����c�卂���w�@�@�i�q�T�N�j�@������ | �S | ���{���O���Z�@�i�q�T�N�j�@���� | |||||||||||||||||
 �@������y��x2�c�A ����y��ax�{2a�c�C �@������y��x2�c�A ����y��ax�{2a�c�C����y��(3��2�|4)x�{6��2�|8�c�E (1) a�̒l�����߂�B �y���z�A���,A(�|1,1) �C��A(�|1,1)��������,1���|a�{2��, a��1 (2) EA/EB �̒l�����߂�B �y���z�A���C���,B(2,4)�@�E���E(�|2,0)
�y���z�A���E���x2��(3��2�|4)x�{6��2�|8 ����������ď��������̉���, x����2�|2 (4) �l�p�`ACBD�̖ʐς����߂�B �y���zC(��2�|2,6�|4��2)�@D(2��2�|2,12�|8��2) F(2��2,2��2)��,FD��10��2�|12 ��EBD�� �@�� �@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�E�ւÂ����j |
 �@�����@�ƕ������A��2�_A,B�Ō�����Ă���B �@�����@�ƕ������A��2�_A,B�Ō�����Ă���B(1) �_B�̍��W�����߂Ȃ����C �y���z�Ay��ax2�ɂ`(4,8)���������,a�� �A��y�� (2) �_B�ƌ��_O�ɂ��đΏ̂ȓ_��D�Ƃ���Ƃ�,��ADB�̖ʐς����߂Ȃ����B �y���zD(2,�|2) ��ADB�������`�|3�̎O�p�` �@��10�~6�|10�|8�|18��60�|36��24cm2 (3) �_B���璼��AD�Ɉ����������̒��� �y���zAD����22�{102��2��26 ��ADB��
|
|||||||||||||||||||
�@(2)�Ɠ��l�ɂ���,EC/ED��
|
||||||||||||||||||||
| �Q | �������Z�@�iR�U�N�j�@������ | �T | �����啍�����Z�@�iR�U�N�j�@������ | |||||||||||||||||
 �@������y��x2�c�A�ƒ���y��x�{6�c�C �@������y��x2�c�A�ƒ���y��x�{6�c�C(1) �_A,B�̍��W�����߂�B���݂̂ł悢�B �y���z�A���C���,x2��x�{6 x���|2,3��, A(�\2,4) B(3,9) (2) a�̒l�Ɠ_�c�̍��W�����߂�B �y���zD(d,d2)�Ƃ����,C,D�̒��_�̓C���,
(3) �_�c��ʂ�,�l�p�`ACBD�̖ʐς��Q�������钼���̎� �y���zDB//AE�ƂȂ�_�d(3,4)���Ƃ��, �@2��������DE��, y���| |
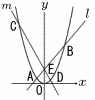 �@AE:EB��1:3�̂Ƃ�, �@AE:EB��1:3�̂Ƃ�,(1) ����l�̎������߂Ȃ����B �y���zA(�|t,t2)�Ƃ����,B(3t,9t2)
(2)���`�d�b�Ɓ��c�d�a�̖ʐϔ䂪2:1�̂Ƃ�, (�A) �_�c��x���W�����߂Ȃ����B �y���zCE:ED��1:k�Ƃ����,��AEC�Ɓ�DEB��(1�~1):(3�~k) �@1:3k��2:1���,k�� C(�|s,s2)�Ƃ���,(1)�Ɠ��l�Ɍv�Z�����, ks�� (�C) ����m�̎������߂Ȃ����B �y���z y��(k�|1)sx�{ks2��,k�� �����m��, y���| |
|||||||||||||||||||
| �R | �����V�����Z�@�iR�V�N�j�@���� | 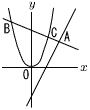 (3) �_C��y���W��,a��p���ĕ\���Ȃ����B (3) �_C��y���W��,a��p���ĕ\���Ȃ����B�y���z
�@����y��(3�{a)(x�|3)�{9��(3�{a)x�|3a��,�@�|3a (4) ��OAB�̖ʐς� �y���z��OAB����AOC�{��BOC ���ʒ��OC���|3a�@�c�A �����̘a��A��B��x���W����3�|a�c�C �A�C���,��OAB�� �@a2�|3a�|1��0���, a��\(\color{red}{\frac{3-\sqrt{13}}{2}}\) |
||||||||||||||||||
| �@��y��x2�̃O���t���2�_A,B������,�_A��x���W��a,�_B��x���W��3�ł��B �܂�,����AB��y���̌�_��C�Ƃ��܂��B������,a��0�Ƃ��܂��B (1) a���|2�̂Ƃ�,�_C��y���W�����߂Ȃ����B �y���z A(�|2,4) B(3,9)���,y��x�{6��,�@6 (2) ��OBC�̖ʐς���OAC�̖ʐς�2�{�ɂȂ�Ƃ�,�_C��y���W�����߂Ȃ����B �y���z���OC�����ʂ�����,����(x���W)��2�{ (�|a)�~2��3���,a���| A(�| �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�E�ւÂ����j |
||||||||||||||||||||