| 1 |
久留米大附設高校 (R5年) ★★★ |
5 |
東大寺学園高校 (R5年) ★★★ |
x,yについての2つの連立方程式
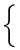 |
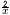 |
+ |
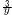 |
=−5 |
|
と |
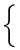 |
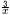 |
− |
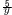 |
=21 |
|
が同じ解 |
| ax+by=2 |
bx+ay=−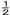 |
をもつとき, 解 x, yと定数 a, bの値をそれぞれ求めよ。
|
a,bを定数とする。x,yについての連立方程式
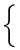 |
ax+4by=−1 |
の解と |
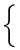 |
2x+3y=3 |
の解が |
| x+2y=1 |
x+by=a |
一致するとき,a, bの値を求めよ。
|
| 2 |
国立高専 (R7年) ★★ |
6 |
立教新座高校 (R5年) ★★★ |
| 2つの連立方程式 |
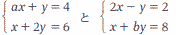 |
の解が |
同じであるとき, a=[ ], b=[ ]である。
|
a,bは定数とします。
| 太郎君は連立方程式 |
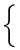 |
3x−7y=16 |
を解き, |
| ax+by=1 |
| 花子さんは連立方程式 |
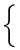 |
bx−ay=−38 |
を解き |
| 4x+y=−7 |
ました。
このとき,花子さんが求めたxの値は,太郎君が求めたyの値の4倍で,花子さんが求めたyの値は,太郎君が求めたxの値の3倍でした。a, bの値を求めなさい。
|
| 3 |
西大和学園高校 (R7年) ★★★ |
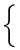 |
2x+5y=21 |
を解いて得られる解のうち, |
| (2x−3)2+(y−5)2=1 |
x,yともに整数である解を求めよ。
|
| 4 |
東京工大附属科技高校 (R6年) ★ |
7 |
愛光高校 (R6年) ★★★ |
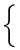 |
(2a−1)x+(b+1)y=−3 |
| (2b+1)x−(a−1)y=11 |
の解がx=−1,y=2であるとき,定数a,bの値をそれぞれ求めなさい。
|
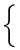 |
4x+y=−3 |
の解のxとyの値を入れかえると, |
| −ax+by=3 |
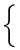 |
ax+by=11 |
の解になる。このとき,a,bの値 |
| 7x+16y=3 |
を求めよ。
|