| 1 |
久留米大附設高校 (R5年) ★★★ |
5 |
東大寺学園高校 (R5年) ★★★ |
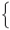 |
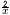 |
+ |
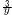 |
=−5…ア |
|
と |
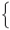 |
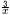 |
− |
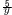 |
=21…ウ |
|
が |
| ax+by=2…イ |
bx+ay=−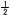 …エ …エ |
同じ解をもつとき,x,yとa,bの値をそれぞれ求めよ。
【解】まず,a,bを含まない式で計算
アとウを連立させて解くと, x= , y=− , y=−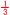
| これをイ,エに代入すると, |
 |
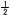 a− a−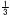 b=2 b=2 |
−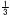 a+ a+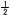 b=− b=−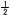 |
これを解いて, a=6, b=3 |
 |
ax+4by=−1…ア |
と |
 |
2x+3y=3…ウ |
の |
| x+2y=1…イ |
x+by=a…エ |
解が一致するとき,a, bの値を求めよ。
【解】まず,a,bを含まない式で計算
イとウを連立させて解くと, x=3, y=−1
| これをア,エに代入すると, |
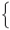 |
3a−4b=−1 |
| 3−b=a |
これを解いて, a=11/7, b=10/7 |
| 2 |
国立高専 (R7年) ★★ |
6 |
立教新座高校 (R5年) ★★★ |
| 2つの連立方程式 |
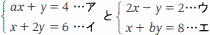 |
の解が同じであるとき, a=[ ], b=[ ]である。
【解】
イウを連立させて解くと, x=2,y=2…オ
| オをアエに代入すると, |
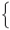 |
2a+2=4 |
| 2+2b=8 |
これを解いて, a=1, b=3 |
| 太郎君は |
 |
3x−7y=16…ア |
を解き, |
| ax+by=1…イ |
| 花子さんは |
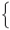 |
bx−ay=−38…ウ |
を解きました。 |
| 4x+y=−7…エ |
このとき,花子さんが求めたxの値は,太郎君が求めたyの値の4倍で,花子さんが求めたyの値は,太郎君が求めたxの値の3倍でした。a, bの値を求めなさい。
【解】
求めた解を,
太郎君は(x1,y1),花子さんは(x2,y2)とすると,
x2=4y1, y2=3x1…オ
これをエに代入すると, 4・4y1+3x1=−7…カ
またアより, 3x1−7y1=16…キ
カ,キを連立させて解くと,x1=3, y1=−1…ク
これをオに代入すると, x2=−4, y2=9…ケ
ク,ケをイ,ウに代入して,
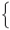 |
3a−b=1 |
で,a=2,b=5 |
| −4b−9a=−38 |
|
| 3 |
西大和学園高校 (R7年) ★★★ |
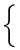 |
2x+5y=21 …ア |
を解いて得られる解の, |
| (2x−3)2+(y−5)2=1…イ |
うち,x,yともに整数である解を求めよ。
【解】イより,(2x−3, y−5)=(0,±1)または(±1,0)
よって,整数解は,(x,y)=(−1,5),(−2,5)…ウ
ウのうちアも満たすのは, x=−2, y=5 |
| 4 |
東京工大附属科技高校 (R6年) ★ |
7 |
愛光高校 (R6年) ★★★ |
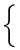 |
(2a−1)x+(b+1)y=−3…ア |
| (2b+1)x−(a−1)y=11 …イ |
の解がx=−1,y=2であるとき,定数a,bの値をそれぞれ求めなさい。
【解】解をア,イに代入
アより,a−b=3 …ウ
イより,a+b=−5…エ
ウとエを連立させて解くと, a=−1, b=−4
|
 |
4x+y=−3 |
の解のxとyの値を入れかえると, |
| −ax+by=3 |
 |
ax+by=11 |
の解になる。このとき,a,bの値を求めよ。 |
| 7x+16y=3 |
【解】解の値を入れかえなければ
 |
4x+y=−3…ア |
と |
 |
bx+ay=11…ウ |
は共通解をもつ |
| −ax+by=3…イ |
16x+7y=3…エ |
アとエを連立させて解くと, x=−2,y=5
| これをイ,ウに代入して, |
 |
2a+5b=16…イ' |
| 5a−2b=11…ウ' |
イ'とウ'を連立させて解いて, a=3,b=2 |