| 32 塗り分け (略解) |
| 32 塗り分け (略解) |
| 1 | 神奈川県立高校/特色 (R5年) ★★★ | 4 | 大阪星光学院高校 (R4年) ★★★ |
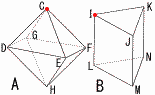 (1) 2つを選んで赤く着色し印をつけるとき, (1) 2つを選んで赤く着色し印をつけるとき,【解】 A…Cと他の1点を選ぶとき, ・Cと(D,E,F,G)は回転同位置で,1通り ・CとHで1通り よって,Aは1+1=2通り B…Iと他の1点を選ぶとき, ・Iと(J,K)は回転同位置で,1通り ・IとLで1通り ・Iと(M,N)で2通り よって,Bは1+1+2=4通り (2) 3つを選んで赤く着色し印をつけるとき, 【解】 A…Cと他の1点を選ぶとき, ・Cと(DE,EF,FG,GD)は回転同位置で,1通り ・Cと(DF,EG,DH,EH,FH,GH)は回転同位置で,1通り よって,Aは1+1=2通り B…Iと他の1点を選ぶとき, ・IとJKで1通り ・上面から2点,下面から1点は回転同位置で,1通り ・Iと(JL,JM)で2通り よって,Bは1+1+2=4通り |
各領域を赤,青,黄の3色使って塗り分ける。ただし,3色すべての色を使うものとし,隣り合う領域には同じ色を塗らないようにする。 (1) 図1の1〜4の領城を塗り分ける方法は[ ]通りある。 【解】3色で3か所(2パターン) (3×2×1)×2=(3×2×1)×5=30通り 【解】塗り分け方は右図 これが回転して,aは1〜5の5パターン (3×2×1)×5=30通り 【解】塗り分け方は右図 ア 回転して3パターン イ 回転して1パターン ウ 回転して6パターン ア〜ウより,(3×2×1)×10=60通り |
||
| 2 | 滝川高校 (R6年) ★★ | 5 | 慶應義塾志木高校 (R4年) ★★★ |
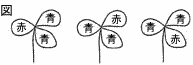 花子さんと太郎さんは図の図案において,花びら1枚ずつに色鉛筆で色を塗ることにした。色鉛筆は赤,青,黄の3色が1本ずつある。 花子さんと太郎さんは図の図案において,花びら1枚ずつに色鉛筆で色を塗ることにした。色鉛筆は赤,青,黄の3色が1本ずつある。[ ]にあてはまる数を記入しなさい。 【解】赤R,青B,黄Yとして, ア RRB RBB BBY BYY YYR YRRそれぞれ3通りで, 3×6=18通り イ RBY RYB BRY BYR YRB YBR の6通り ウ 3×3×3=27通り |
立方体の6面をぬり分けるとき (1) 上面を赤とし,残りを5色で 底面は,赤以外の5通り 側面は回転で二重になっているから, 5×(4×3×2×1÷4)=30通り 上・底面(5通り)→側面(6通り) 上下反転で二重になっているから, 5×6÷2=15通り (3) どれか2面は同色 ア 2面が隣り合わないとき,(2)より15通り イ 2面が隣り合うとき,残りを4色で 上下反転で二重になっているから, 5×(4×3×2×1)÷2=60 アイより,15+60=75通り |
||
| 3 | 雲雀丘学園高校 (R7年) ★★★ | 【解】5進数表記と考えられる 312(5)=3×52+1×5+2=75+5+2=82 (2) 4か所だけぬることで表される数は何個あるか。 【解】a+b+c=4の整数解(a,b,c)の組の個数 ・(0,0,4)型は3個 ・(0,1,3)型は6個 ・(0,2,2)型は3個 ・(1,1,2)型は3個 よって全部で,3+6+3+3=15個 (3) 6か所だけぬりで,各位の数が同じものをすべて求めよ。 【解】14〜125のうち,候補は22,33,…,99,111 22=42(5), 33=113(5), 44=134(5), 44=134(5), 55=210(5) 66=211(5), 77=302(5), 88=323(5), 99=344(5), 111=421(5) よって6か所は,下線で, 22と66 |
|
それぞれ4分割された白色の正方形が3枚ある。これらの正方形に次のように色をぬることで数を表すこととする。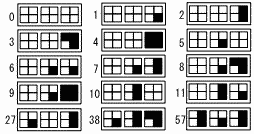 (→右へつづく) (→右へつづく) |
|||