 データの活用 |
２５ コイン (確率) （解答） |
| 以下の問題では,どのコインも表と裏の出方は同様に確からしいものとします。 | |
| データの活用 |
２５ コイン (確率) （解答） |
| 以下の問題では,どのコインも表と裏の出方は同様に確からしいものとします。 | |
| １ | 明大付属八王子高校 （Ｒ５年） ★★ | ５ | 都立八王子東高校 （Ｒ７年） ★ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 100円硬貨と50円硬貨が2枚ずつあります。この4枚の硬貨を同時に投げるとき,表が出た硬貨の合計金額が100円以上200円以下となる確率を求めなさい。【解】4枚の表裏の出方は, 24＝16通り 100〜200円は,表より10通り よって,確率＝10÷16＝  |
表に1,裏に2と書かれた赤色,青色,黄色の硬貨が1枚ずつ,計3枚ある。この硬貨3枚を同時に投げたとき,出た面に書かれた数の積が素数になる確率を求めよ。 【解】3枚の数の出方は全部で,23＝8通り 積が素数は, (赤,青,黄)＝ (1,1,2) (1,2,1) (2,1,1) の3通り 確率＝3/8 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ２ | 日本大第二高校 （Ｒ６年） ★ | ６ | 佼成学園高校 （Ｒ５年） ★ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
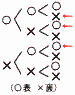 1枚の硬貨を3回投げる。それぞれの出方に対して表が出れば1点,裏が出れば2点を与えるものとする。得点の合計が5点となる確率を求めよ。【解】5点となるのは,表2回裏1回 樹形図より,確率＝  |
1枚のコインを3回投げる。表が出たときは200円もらえ,裏が出たときは100円払うゲームをするとき,ゲーム開始時と所持金が変わらない確率を求めなさい。 【解】表裏の出方は全部で,23＝8通り 表(〇)2回と裏(×)1回出ればよいから, 出方は (〇××) (×〇×) (××〇) の3通りで,確率＝3/8 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ３ | 慶應義塾志木高校 （Ｒ５年） ★★★ | ７ | 学習院高等科 （Ｒ６年） ★★ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(1) 表が1回以上出る確率 【解】(表が1回以上)の確率＝1−(すべて裏)の確率 確率＝1−(  )6＝63/64(2) 表が連続して3回以上出る確率 【解】右表参照 (空欄は表裏どちらでもよい) ・3回連続＝4＋2＋2＋4＝12通り ・4回連続＝2＋1＋2＝5通り ・5回連続＝1＋1＝2通り ・3回連続＝1通り 確率＝(12＋5＋2＋1)÷64＝5/16 |
１枚のコインを投げて,同じ面が連統して3回出た時点で終了となるゲームを行う。例えば,コインを投げて1回目に表,2回目に裏,3回目に裏が出たとき,4回目に表が出た場合はゲームを続行し,裏が出た場合は3回連統して裏が出たのでゲームを終了する。このとき,次の確率を求めなさい。 (1) 3回目にゲームが終了する確率 【解】(〇〇〇)か(×××)の2通り 確率＝2÷23=2/8＝1/4 (2) 5回目にゲームが終了する確率 【解】以下の4通り (〇×〇〇〇) (××〇〇〇) (〇〇×××) (×〇×××) 確率＝4÷25＝4/32＝1/8 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ４ | 桐光学園高校 （Ｒ６年） ★★★ | ８ | 龍谷大付属平安高校 （Ｒ７年） ★★ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
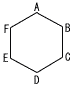 一辺が1cmの正六角形ABCDEFの辺上を2点P,Qが時計回りに動く。はじめ,点Pは点Aにあり,点Qは点Dにある。点Pはコインを投げるごとに表が出れば1cm,裏が出れば2cmずつ動く。点Qはコインを投げるごとにコインの表裏に関わらず3cmずつ動く。 (1) 2回投げるとき,PとQが同じ頂点にある確率を求めよ。【解】Qは2回でD PがDになるには,表裏1回ずつ 樹形図より,確率＝  (2) 3回投げるとき,PとQが同じ頂点にある確率を求めよ。 【解】Qは3回でA PがAになるには,裏が3回 樹形図より,確率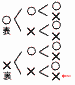＝   (3) コインを6回投げるとき,PとQが少なくとも1回は同じ頂点にある確率を求めよ。【解】余事象(すべて異なる頂点)で考える QはADADADだから,余事象のPは次の11通り BCDEFA, BCDEFB, BCDFBC, BCEFBC, BCEABC, BCEACE, CEFABC ,CEFACE, CEFBCE, CEFBDE, CEFBDF よって,確率＝1−11/26＝53/64 |
 硬貨を5回投げ,表が出たときは赤,裏が出たときは青で,右の図のような5つの文字を左から順に壁るとき,(1) 両端を赤で塗る確率を求めなさい。 【解】表裏の出方は全部で,25＝32通り 3文字ELAの塗り方は23＝8通りで, 確率＝8÷32＝1/4 (2) 色を交互に塗る確率を求めなさい。 【解】(赤青赤青赤)か(青赤青赤青)の2通りで 確率＝2÷32＝1/16 (3) 3文字以上赤で塗る確率を求めなさい。 【解】3パターンで ・赤5青0…1通り ・赤4青1…5通り
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||