 データの活用 |
１９ カード (確率) ２ （略解） |
| 以下の問題では,どのカードが引かれることも同様に確からしいものとします。 | |
| データの活用 |
１９ カード (確率) ２ （略解） |
| 以下の問題では,どのカードが引かれることも同様に確からしいものとします。 | |
| １ | 埼玉県立高校 （Ｒ７年） ★★ | ５ | 国士館高校 （Ｒ５年） ★★ | ||||||||||||||||||
 右の図のような,5枚のカードがあります。この5枚のカードを箱に入れて,そこから1枚ずつ合計で2枚取り出します。1枚目に取り出したカードの数をx,2枚目に取り出したカードの数をyとするとき,\(\frac{1}{x}\)＋\(\frac{1}{y}\)の値が 以上1以下 となる確率を求めなさい。ただし,箱の中は見えず,取り出したカードは箱に戻さないものとします。 【解】2枚の取り出し方は全部で,5×4÷2＝10通り 条件に合うのは,  ＋ ＝ ,＋ ＝ ,＋ ＝ の3通りゆえに,確率＝  |
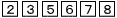 右の図１のように,A,B,C,D,Eのアルファベットが1つずつ書かれた5枚のカードが箱の中に入っている。 右の図2は,正三角形ＡBCの辺AB,BC,CAの中点をそれぞれD,E,Fとしたものである。箱の中から同時に2枚のカードを取り出し,カードに書かれたアルファペットに対応する2点と点Pをそれぞれ結ぶ。 (1) 三角形ができない確率を求めなさい。 【解】2枚のカードを取り出し方は全部で,5×4÷2＝10通り できないのは(A,C)の1通りで, 確率＝  (2) 次のア～ウの三角形になる確率を考える。 ア～ウのうち,それになる確率がもっとも小さいものを選び,その記号を書きなさい。また,その確率を求めなさい。 ア 正三角形 イ 直角三角形 ウ 正三角形でない二等辺三角形 【解】ア3, イ2, ウ4で, 小さいのはイ イの確率＝2/10＝  |
||||||||||||||||||||
| ２ | 大阪教育大附属池田校舎 （Ｒ６年） ★★ | ||||||||||||||||||||
| 1,2,3,4の番号がそれぞれ書かれたカードが4枚ある。4枚のカードのうち,3枚を選び,順番に横に並べ,3桁の自然数をつくる。カードを並べてできる自然数が11の倍数になる確率を求めなさい。 【解】3桁の自然数全部では,4×3×2＝24通り このうち,11の倍数は,132 231 143 341 の4通り よって,確率＝4÷24＝  |
|||||||||||||||||||||
| ３ | 慶應義塾高校 （Ｒ５年） ★★★ | ６ | 京都市立西京高校 （Ｒ７年） ★★ | ||||||||||||||||||
| カードに 1⃣ 2⃣ 3⃣ 4⃣ 6⃣ の数が書かれた5枚の中から1枚とって出た数を記録して元に戻す。 (1) 3つの数の積xyzが偶数となる確率 【解】偶数の確率＝1－奇数の確率
【解】因数として,3が2個以上
(3) xyzが8の倍数となる確率 【解】因数として,4または2×6 4以外を〇,2か6を△,1か3を□とすると, ・(4,4,4)は1通り ・(4,4,〇)は12通り ・(4,△,△)は12通り ・(4,△,□)は24通り ・(△,△,△)は8通り 確率＝(1＋12＋12＋24＋8)÷125＝57/125 |
袋の中に1から9までの番号が1つずつ書かれたカード9枚が入っている。袋から無作為に1枚のカードを取り出し,番号を記録してカードを袋に戻す操作を考える。 (1) 1回の操作で取り出された数を2乗して5で割り切れる確率を求めよ。 【解】5のみで, 確率＝1/9 (2) 1回の操作で取り出された数を2乗して5で割った余りが4となる確率を求めよ。 【解】2,3,7,8の4通りで, 確率＝4/9 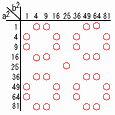 (3) 操作を2回行い記録された数を順にa,bとする。a2＋b2が5で割り切れる確率を求めよ。 【解】(右図参照) 確率＝33/92＝11/27 |
||||||||||||||||||||
| ４ | 愛光高校 （Ｒ７年） ★★ | ７ | ラ・サール高校 （Ｒ７年） ★★★ | ||||||||||||||||||
| の5枚のカードから1枚引き,書かれている数字を記録した後に元に戻すという操作を３回繰り返したとき, (1) 記録した数字の最小値が2以上である確率を求めよ。 【解】すべて2以上の場合 確率＝(4/5)3＝64/125 (2) 記録した数字の最小値が2で最大値が4である確率を求めよ。 【解】(2,2,4)が3通り, (2,3,4)が6通り, (2,4,4)が3通り 全部で12通りだから, 確率＝12/53＝12/125 |
6枚のカード3,4,4,5,5,5をすべて裏返してよく混ぜてから1枚ずつ計4枚めくり,出た数字を順にa,b,c,dとする。 (1) Ｘ＞2025となる確率 【解】a＝b＝5のとき 確率＝(3枚の5から2枚選ぶ方法)÷(6枚から4枚選ぶ方法) ＝3÷15＝ (2) Ｘが5の倍数となる確率 【解】c×dが5の倍数のとき 確率＝1－(c,dが3か4の確率)＝1－3/15＝  (3) Ｘが9の倍数となる確率 【解】ab＋cdが9の倍数のとき, (5×5＋5×4＝45) (a,b,c,d)＝(4,5,5,5) (5,4,5,5) (5,5,4,5) (5,5,5,4)が各12通り 確率＝(12×4)÷(6×5×4×3)＝48/360＝2/15 |
||||||||||||||||||||
