 データの活用 |
１７ さいころ (確率) ３ （略解） |
| 以下の問題では,さいころは,どの目が出ることも同様に確からしいものとします。 | |
| データの活用 |
１７ さいころ (確率) ３ （略解） |
| 以下の問題では,さいころは,どの目が出ることも同様に確からしいものとします。 | |
| １ | 中央大附属横浜高校 （Ｒ７年） ★ | ６ | 慶応義塾女子高校 （Ｒ７年） ★★ | ||||||||||||||||||
| サイコロを2個投げて,出た目の数の和をXとする。Xと16の最大公約数が4となる確率を求めなさい。 【解】X＝4,12 2数は, (1,3) (2,2) (3,1) (6,6) の4通りで,4/36＝  |
大小のさいころを同時に投げるとき,大きいさいころの目をa,小さいさいころの目をbとする。直線y＝－ax＋\(\sqrt{2b}\)とx軸とy軸で囲まれた三角形の面積をSとして, (1) Sをa,bを用いて表しなさい。 【解】x切片は(\(\frac{\sqrt{2b}}{a}\),0) y切片は(0,\(\sqrt{2b}\)) S＝  ×\(\sqrt{2b}\)×\(\frac{\sqrt{2b}}{a}\)＝\(\color{red}{\frac{b}{a}}\)(2) S＝1となる確率を求めなさい。 【解】S＝\(\frac{b}{a}\)＝1より,a＝b (a,b)＝(1,1,) (2,2) … (6,6) の6通りで,6/62＝  (3) tを1より大きい実数とする。S＝tとなる確率が\(\frac{1}{36}\)より大きくなるとき,tの値として考えられるものをすべて求めなさい。 【解】t＝\(\frac{b}{a}\)＞1より,t＝2,3,…,6,  , , , , , このうち\(\frac{1}{36}\)より大きいのは,  ,2,3 |
||||||||||||||||||||
| ２ | 桜美林高校 （Ｒ７年） ★ | ||||||||||||||||||||
| 6つの面に書かれた数字が1,1,1,2,2,3である特殊なさいころがある。このさいころを2回投げるとき,出た目の数の和が偶数である確率を求めなさい。 【解】(奇＋奇)または(偶＋偶)のとき (  )2＋( )2＝5/9 |
|||||||||||||||||||||
| ３ | 四天王寺高校 （Ｒ５年） ★★ | ７ | 立教新座高校 （Ｒ７年） ★★★ | ||||||||||||||||||
| Aの出た目の数をa,Bの出た目の数をbとします。 (1) √ab＜5をみたす確率 【解】ab＜25で, (a,b)≠(5,5) (5,6) (6,5) (6,6) 32通りで, 確率＝32÷36＝ 
確率＝3÷36＝ 
確率＝8÷36＝  |
1個のさいころを4回投げて,1回目に出た目の数を千の位,2回目に出た目の数を百の位,3回目に出た目の数を十の位,4回目に出た目の数を一の位の数とする4けたの整数をつくる とき,次のような整数ができる確率を求めなさい。 (1) 5の倍数 【解】一位が5であればよいから, (2) 4の倍数 【解】下3桁が4の倍数であればよい 12,16,24,32,44,52,56,64の9通りで, 9/36＝  (3) 1221のように,2種類の数字を2つずつ用いて表される整数
(4) 各位の数の和が10以上の整数 【解】1－(和が10未満の確率) ・〇〇〇〇型…1111,2222の2通り ・〇〇〇△型…1112,1113等の7通り ・〇〇△△型…1122,1133の2通り ・〇〇△×型…1123,1124等の7通り 和が10未満＝1×2+4×7+6×2+12×7＝126 よって,1－(126/64)＝1－(126/1296)＝65/72 |
||||||||||||||||||||
| ４ | 都立日比谷高校 （Ｒ７年） ★★ | ||||||||||||||||||||
| 1から6までの目が出る大小1つずつのさいころを同時に1回投げる。 大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとするとき, a＞bが成り立ち,(a＋1)2－(b＋1)2が3の倍数となる確率を求めよ。 【解】(a＋1)2－(b＋1)2＝(a－b)(a＋b＋2)が3の倍数 a＞b…ア (a－b)が3の倍数より,a－ｂ＝3…イ (a＋b＋2)が3の倍数より,a＋b＝4,7,10…ウ アイウより,(a,b)＝(3,1) (6,1) (5,2) (4,3) (6,4) (4,1) (6,3)の7通り よって, 7/36 |
|||||||||||||||||||||
| ５ | 駿台甲府高校 （Ｒ６年） ★★ | ８ | 明治学院高校 （Ｒ６年） ★★ | ||||||||||||||||||
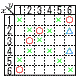 1から6までの目が出るさいころ1個を2回投げて,1回目に出た目をx,2回目に出た目をyとする。(1) xy＝6となる確率を求めよ。 【解】表(〇)より4通りで,確率＝  (2) x2－xy＋8＝0となる確率を求めよ。 【解】式変形して,y＝x＋  表(△)より2通りで,確率＝  (3) x2－6x＝y2－6yとなる確率を求めよ。 【解】式変形して,(x－y)(x＋y－6)＝0 x＝yまたはx＋y＝6を満たすのは表(×)で,確率＝5/18 |
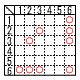 2つのさいころA,Bを同時に１回投げて,出た目をそれぞれa,bとする。a,bの最小公倍数をＸとするとき,(１) Ｘ＝6となる確率を求めよ。 【解】表(〇)より9通りで,確率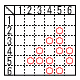＝   (2) Ｘ＞6となる確率を求めよ。 【解】表(〇)より12通りで,確率＝  |
||||||||||||||||||||
