データの活用	１６　さいころ (確率) ２　（略解）
以下の問題では,さいころは,どの目が出ることも同様に確からしいものとします。

１	群馬県立高校　（Ｒ６年）　★	５	都立立川高校　（Ｒ６年）　★
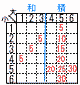大きいさいころの目が3以下のときは2つのさいころの目の和をXとし,大きいさいころの目が4以上のときは2つのさいころの目の積をXとする。このとき,Xが5の倍数となる確率を求めなさい。 【解】表より11通りで,確率＝11/36		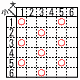大きいさいころの出た目の数を十の位の数,小さいさいころの出た目の数を一の位の数とする2桁の整数をつくる。つくった整截を4で割った余りか3である確率を求めよ。 【解】表より9通りで,確率＝
２	京都府立嵯峨野高校　（Ｒ７年）　★	６	大阪府立高校C　（Ｒ７年）　★★
出た目 角度 1 15° 2 30° 3 45° 4 60° 5 75° 6 90° 　1から6までの目が出るさいころを投げ,右の対応表にもとづいて角度を決める。さいころを3回投げたとき,1回目の角度をa, 2回目の角度をb, 3回目の角度をcとする。このとき,a,b,cを3つの内角の角度とする直角三角形ができる確率を求めよ。 【解】a＋b＋c＝180 ・(15,75,90)型…6通り　　・(30,60,90)型…6通り ・(45,45,90)型…3通り 　よって,(6＋6＋3)÷63＝15/216＝5/72		A,B二つのさいころを同時に投げ,Aのさいころの出る目の数をa,Bのさいころの出る目の数をbとし,c＝ 2a＋bとする。このとき,\(\frac{2025}{c}\)の値が自然数である確率はいくらですか。 【解】2025＝34×52だから,ｃ＝3,5,9,15 ・c＝3のとき,(a,b)＝(1,1) ・c＝5のとき,(a,b)＝(1,3) (2,1) ・c＝9のとき,(a,b)＝(2,5) (3,3) (4,1) ・c＝15のとき,(a,b)＝(5,5) (6,3) 　よって,8÷62＝
３	甲南高校　（Ｒ７年）　★★	７	札幌日大高校　（Ｒ７年）　★★
１つのさいころを２回続けて投げて,１回目に出た数をa,2回目に出た数をbとする。 (1) \(\sqrt{ab}\)が整数となる(a,b)の組は何通りか。 【解】ab＝1,4,9,16,25,36 (a,b)＝(1,1) (1,4) (2,2) (4,1) (3,3) (4,4) (5,5) (6,6) の8通り (2) xについての方程式ax＝bの解が整数となる碓率を求めよ。 【解】aがbの約数 表より14通りで,14÷62＝7/18 (3) \(\frac{1}{a}\)＋\(\frac{1}{b}\)の値が１以下になる確率を求めよ。 【解】余事象で考える,　1−(1より大きくなる確率) (a,b)＝(1,1)〜(1,6) (6,1)〜(2,1) の11通り 　よって,1−(11/36)＝		\(\sqrt{11-k}\)が整数となる確率を求めなさい。 【解】11−k＝0,1,4,9(平方数)より,k＝2,7,10,11 ・k＝2のとき,(大,小)＝(1,1) ・k＝7のとき,(大,小)＝(1,6) (2,5) (3,4) (4,3) (5,2) (6,1) ・k＝10のとき,(大,小)＝(4,6) (5,5) (6,4) ・k＝11のとき,(大,小)＝(5,6) (6,5) 　よって,12÷62＝
		８	灘　高校　（Ｒ７年）　★★★
		2つのさいころの出た目が異なるとき小さい方の目を得点し,2つのさいころ出ｉた目が同じときは得点を与えない。この操作を2回行ったとき,得点の合計が5点となる確率は[　　]である。 【解】右の得点表参照 ・0→5点,5→0点のとき,(6/36)×(2/36)…ア ・1→4点,4→1点のとき,(10/36)×(4/36)…イ ・2→3点,3→2点のとき,(8/36)×(6/36)…ウ 　(ア＋イ＋ウ)×2＝(12＋40＋48)/362×2＝25/162
４	ラ・サール高校　（Ｒ６年）　★★	９	立教新座高校　（Ｒ６年）　★★★
大,中,小の3個のサイコロを同時に投げ,出た目の数をそれぞれa,b,cとする。次のようになる確率をそれぞれ求めよ。 　　　　　　　　　　　　　　　　　 c 1 2 3 4 5 6 計 ab 1 2 2 3 2 4 14 (1) ab＝c 【解】cが1〜6のとき,abは14通り 　よって,確率＝14÷63＝7/108 c 1 2 3 4 5 6 計 a+2b 0 0 1 1 2 2 6 （2） a＋2b＝c 【解】cが1〜6のとき,abは14通り 　よって,確率＝6÷63＝1/36 （3） aを百の位,bを十の位,cを一の位としてできる3けたの整数が9の倍数になる。 【解】a＋b＋c＝9,18 (a,b,c)＝(1,2,6) (1,3,5) (2,3,4) が各6通り (a,b,c)＝(1,4,4) (2,2,5) が各3通り (a,b,c)＝(3,3,3,) (6,6,6,)が各1通り 　よって,確率＝(3×6＋2×3＋2×1)÷63＝13/108		,2次方程式ax2＋bx＋c＝0の解について,次の確率を求めなさい。 (1) 2つの解か−2,−3となる確率 【解】(x＋2)(x＋3)＝x2＋5x＋6 (a,b,c)＝(1,5,6)の1通りで,確率＝1÷63＝1/216 b 1 2 3 4 5 6 計 a＋c 0 1 2 3 4 5 15 (2) −1を解にもつ確率 【解】式にx＝−1を代入すると,a＋c＝b bが1〜6のとき,a＋cは15通り b2 1 4 9 16 25 36 計 4ac 0 1 0 3 0 1 5 　よって,確率＝15÷63＝5/72 (3) 解が1つになる確率 【解】判別式より,b2＝4ac k 0 1 2 3 4 計 b (3) より 3 5 4 6 5 6 ac 2 6 3 8 4 5 5 2 4 2 2 3 2 20 bが1〜6のとき,4acは5通り 　よって,確率＝5÷63＝5/216 (4) 解が有理数になる確率 【解】b2−4ac＝k2(平方数)のとき kが0〜4のとき,acは20通り 　よって,確率＝20÷63＝5/54

［TOP］　［問題に戻る］　　★　中　　★★　やや難　　★★★　難