４１５さいころ１（解答）

データの活用	１５　さいころ１　（略解）
以下の問題では,さいころは,どの目が出ることも同様に確からしいものとします。

１	芝浦工大附属高校　（Ｒ５年）　★	６	成蹊高校　（Ｒ５年）　★
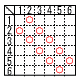大小2個のさいころを同時に投げるとき,出た目が連続する2つの整数となる確率を求めなさい。【解】表より,10通り　10÷36＝5/18		十の位の数がa,一の位の数がbである2桁の整数が6の倍数となる確率を求めよ。【解】12,24,36,42,54,66の6通り　6÷36＝
２	奈良大附属高校　（Ｒ７年）　★★	７	盈進高校　（Ｒ６年）　★★
赤色,青色,黄色の3色のサイコロがある。それらを一回ずつ投げ,赤色のサイコロの出た目をa,青色のサイコロの出た目をb,黄色のサイコロの出た目をcとする。百の位がa,十の位がb,一の位がcである3桁の整数について, (1) abcが偶数となる確率を求めなさい。【解】 c＝2,4,6で,3/6＝ (2) abcが偶数で,さらにa＜b＜cとなる確率を求めなさい。【解】c＝4または6 ・c＝4のとき, 　(3/36)×＝3/216…ア・c＝6のとき, 　(10/36)×＝10/216…ｲア+イより,(3/216)＋(10/216)＝13/216		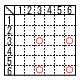1回目,2回目に出た目をそれぞれa,bとする。 (1) aとbがともに3の倍数である確率【解】右表より4通りで, (2) 和a＋bが3の倍数である確率を求めなさい。【解】右下表より12通りで, 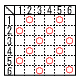(3) ab＋cが3の倍数である確率を求めなさい。【解】3の剰余系で3パターン・ab＝3,6,9,12,15,18,24,30,36 　　　　　　　　　　かつ,c＝3,6の場合　　(2＋4＋1＋4＋2＋2＋2＋2＋1)×2＝40通り・ab＝1,4,10,16,25かつ,c＝2,5の場合　　(1＋3＋2＋1＋1)×2＝16通り・ab＝2,5,8,20かつ,c＝1,4の場合　　(2＋2＋2＋2)×2＝16通り全部で,40＋16＋16＝72通り　　よって, 72÷6³＝
３	都立青山高校　（Ｒ７年）　★★	８	都立隅田川高校　（Ｒ７年）　★
1から6までの目が出る大小1つずつのさいころを同時に1回投げる。大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとするとき,xについての2次方程式ax²＋4x－b＝0 の解が有理数になる確率を求めよ。【解】判別式D＝4＋ab＝9,16(平方数) すなわち,ab＝5,または12になればよいから (a,b)＝(1,5) (5,1) (2,6) (6,2) (3,4) (4,3) の6通りで,6/36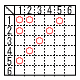＝		1から6までの目が出る大小1つずつのさいころを同時に投げる。大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとして,座標平面上の点 P(a,b)を定める。点Pが一次関数y＝－x＋4のグラフ上にある確率を求めよ。【解】 (a,b)＝(1,4) (2,2) (3,1) の3通りで,3/36＝
４	桜美林高校　（Ｒ６年）　★	９	大阪星光学院高校　（Ｒ７年）　★★
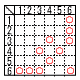図のような,1から6までの番号が書かれた6個のマスがある。大小2つのさいころを同時に投げ,まず,大きいさいころの出た目の数の約数が書かれたマスに〇をつけ,次に,小さいさいころの出た目の数の約数が書かれたマスのうち,まだ〇がつけられていないマスに〇をつける。このとき,4個のマスに〇がつけられている確率を求めなさい。【解】表より,11通りで,11/36		大,中,小の3つのさいころを投げて出た目をそれぞれa,b,cとする。このとき,積abcが5の倍数となる確率は[ア　　　]である。また,a＋b＋c≧15となる確率は[イ　　　]である。ア【解】余事象の確率を利用 1－(5の倍数でない確率)＝1－（すべて1,2,3,4,6の確率) 　＝1－()³＝91/216 イ【解】和a＋b＋c＝15,16,17,1,8 ・和が15のとき, (3,6,6)が3通り,(4,5,6)が6通り,(5,5,5)が1通り・和が16のとき, (4,6,6)が3通り,(5,5,6)が3通り・和が17のとき, (5,6,6)が3通り・和が18のとき, (6,6,6)が1通り　(3×4＋1×2＋6)÷6³＝20/216＝5/54
５	国立音大附属高校　（Ｒ６年）　★
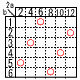大小2個のさいころを同時に投げて,大きいきいころの出た目をa,小さいさいころの出た目をbとする。このとき,2a＋bの値が7の倍数となる確率を求めなさい。【解】表より6通りで,

［TOP］　［問題に戻る］　　★　中　　★★　やや難　　★★★　難