 データの活用 |
１４ 数列３ （略解） |
| データの活用 |
１４ 数列３ （略解） |
| １ | 静岡県立高校 （Ｒ６年） ★ | ５ | 日本大習志野高校 （Ｒ６年） ★ | ||||
【解】4行n列の数は8n よって, 3行n列の数は8n－2 |
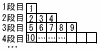 このとき,上から5段目の一番右にある自然数は[ ]であり,2024は上から[ ]段目の一番左から[ ]番目にある。【解】5段目の末項は52＝25 442＜2024＜452より,45段目(1936,1937,…,2025) 45段目には,45×2－1＝89項あって ,88番目 |
||||||
| ２ | 群馬県立高校 （Ｒ５年） ★ | ６ | 明治学院東村山高校 （Ｒ７年） ★★ | ||||
整数a,bと5が,左から規則的に並んでいる。
(1) 20番目の整数は, a ,b, 5 のうちのどれか。 【解】a, 5, b の繰り返し 20÷3＝6余り2 7群の2項目で, 5 (2) 7番目までの和が18, 50番目までの和が121のとき,aとbの値をそれぞれ求めなさい。 【解】 7番目までの和＝2(a＋5＋b)＋a＝18 3a＋2b＋10＝18…ア 50番目までの和＝16(a＋5＋b)＋(a＋5)＝121 17a＋16b＋85＝121…イ アイを連立させて解くと, a＝4, b＝－2 |
以下のように白と黒の碁石を規則的に個数を増やしながら並べます。 ◯◯|●●●●|◯◯◯◯◯◯|●●●●●●●●|◯◯…… (1) 左から50番目の石の色を答えなさい。 【解】各群の最終項は 2, 6, 12, 20, 30, 42,| 56,… 50項は7群（奇数群）だから, 白 (2) 左から150番目の石の色を答えなさい。 【解】n群の最終項はn2＋n 112＋11＜150＜122＋12より,12群(偶数群)だから, 黒 |
||||||
| ７ | 京都成章高校 （Ｒ７年） ★ | ||||||
| １から正の整数nまでのn個の整数の和は\(\frac{n(n+1)}2\)であることが知られている。このとき,101から200までの100個の整数の和を求めなさい。 【解】(1～200の和)－(1～100の和)
|
|||||||
| ３ | 京都府立柴野高校 （Ｒ７年） ★★ | ８ | 愛知高校 （Ｒ５年） ★ | ||||
 紫野高校の郵便番号を調べてみると,603－8231であった。そこで,6,0,3,8,2,3,1の7つの数をこの順にくり返し並べたものを各行に10個ずつ配置し,上から順に第1行,第2行,第3行…とすることにした。(1) 第8行の最後の数を求めなさい。 【解】80÷7＝11余り3より,12群の3番目だから, 3 (2) 第1行の初めの数から第8行の最後の数までのすべての数の和を求めなさい。 【解】(6+0+3+8+2+3+1)×11＋(6+0+3)＝23×11＋9＝262 |
(1) 16番目の数字は[ ]である。 【解】2進数が並んでいる 1111(15番目)の次だから, 10000 (2) 101101は[ ]番目の数字である。 【解】101101(2)＝25＋23＋22＋1＝32＋8＋4＋1＝45番目 (3) 2023番目の数字は[ ]である。 【解】2023を2で割り続け,出た余りを逆順に並べる 2023(10)＝11111100111(2) |
||||||
| ４ | 大阪学院大高校 （Ｒ６年） ★ | ９ | 青山学院高等部 （Ｒ６年） ★★ | ||||
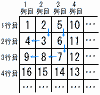 次の図のように,連続する自然数を1から順に規則的に並べていく。(1) 6 行目の1列目の数を答えなさい。 【解】62＝36 (2) 9行目の9列目の数を答えなさい。 【解】92－8＝73 (3) n行目のn列目の数をnを用いて表しなさい。 【解】n2－(n－1)＝n2－n＋1 (4) 101行目の100列目の数を答えなさい。 【解】1012－99＝10201－99＝10102 |
0,1,2,3,4の5種類の数字を用いて作られる正の整数を考える。ただし,同じ数字を繰り返し用いてよいこととする。 これらを小さい方から順に並べると, 1,2,3,4,10,11,12… となる。 (1) 小さい方から数えて24番目の数を求めよ。 【解】1,2,3,4❘10,11,12,13,14❘…❘40,41,42,43,44❘100… 1＋(24－4)÷5＝5だから,5群の末項で, 44 (2) 2024は小さい方から数えて何番目の数か答えよ。 【解】2024(5)＝2×53＋2×5＋4＝264番目 |
||||||