 データの活用 |
１０ 場合の数３ （略解） |
| データの活用 |
１０ 場合の数３ （略解） |
| １ | 桜美林高校 （Ｒ５年） ★★★ | ５ | 四天王寺高校 （Ｒ７年） ★★★  |
|||||||||||
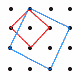 図のように,縦に4個,横に4個の等間隔に並んだ16個の点があり,縦横に隣り合う点どうしの距離は2cmである。これらの点の中からいくつかの点を選び,選んだ点どうしを結んでできる図形について(1) 面積が8cm2の正方形は全部で何個できるか。 ・1辺2√2cm(赤)…4個 (右上図参照) (2) 正方形は全部で何個できるか。 ・1辺2cm…3×3＝9個 ・1辺4cm…2×2＝4個 ・1辺6cm…1個 ・1辺2√2cm(赤)…4個 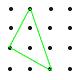 ・1辺2√5cm(青)…2個よって,9＋4＋1＋4＋2＝20個 (3) 面積が10cm2の直角三角形は全部で何個できるか。 ・等辺2√5cmの直角二等辺三角形(緑)…16個 |
１〜10の数字が1つずつ者かれた10枚のカードがあります。 (1) 10枚のカードから同時に3枚のカードを選ぶとき,カードに書かれた数字の和が12になる選び方は[ ]通りあり,積が24になる選び方は[ ]通りあります。 【解】 和12…(1,2,9) (1,3,8) (1,4,7) (1,5,6) (2,3,7) (2,4,6) (3,4,5)の7通り 積24…(1,3,8) (1,4,6) (2,3,4)の3通り (2) 10枚のカードから同時に何枚かのカードを選ぶとき,積が120になる選び方は[ ]通りあります。 【解】120＝23×3×5より,7と9以外を選ぶ 3枚で…(2,6,10) (3,4,10) (3,5,8) (4,5,6) 4枚で…(1,2,6,10) (1,3,4,10) (1,3,5,8) (1,4,5,6) (2,3,4,5) 5枚で…(1,2,3,4,5) よって,4＋5＋1＝10通り (3) 10枚のカードから同時に何枚かのカードを選ぶとき,和が45になる選び方は[ ]通りあります。 【解】45＝(1+2++3+…+10)−10より,和が10を選んだ残り 1枚で…(10) 2枚で…(1,9) (2,8) (3,7) (4,6) 3枚で…(1,2,7) (1,3,6) (1,4,5) (2,3,5) 4枚で…(1,2,3,4) よって,1＋4＋4＋1＝10通り |
|||||||||||||
| ２ | 洛南高校 （Ｒ７年） ★★ | ６ | 渋谷教育学園幕張高校 （Ｒ７年） ★★★ | |||||||||||
| A,B,C,Dの4文字を1列に並べるとき,AとBが隣り合わない並び方は何通りありますか。 【解】4文字の並べ方は,4×3×2×1＝24通り (AB),C,Dの並べ方は,3×2×1＝6通り (AB)の並べ方は2通り よって,24−6×2＝12通り |
白球3個,赤球2個,青球1個のすべての球を,区別のつかない3つの袋に入れることを考えます。ただし,空の袋はつくらない。 (1) すべての袋に白球が入るような,6個の球の袋への入れ方は何通りありますか。 【解】先にW1個ずつを入れ,次にR2個B1個を入れる (0,0,WWB), (0,WW,B), (0,W,WB), (W,W,B)で, 4通り (2) 6個の球の袋への入れ方は全部で何通りありますか。 【解】個数の割り振りは,(1,1,4) (1,2,3) (2,2,2)の3パターン ・(1,1,4)…(W,W,〇) (W,R,〇) (W,B,〇) (R,R,〇) (R,B,〇)の5通り ・(1,2,3)…(W,WW,〇) (W,WR,〇) (W,WB,〇) (W,RR,〇) (W,RB,〇) (R,WW,〇) (R,WR,〇) (R,WB,〇) (R,RB,〇) (B,WW,〇) (B,WR,〇) (B,RR,〇)の12通り ・(2,2,2)…(WW,WR,RB) (WW,WB,RR) (WR,WR,WB)の3通り ゆえに,5＋12＋3＝20通り |
|||||||||||||
| ３ | 久留米大附設高校 （Ｒ７年） ★★ | |||||||||||||
| １個のさいころを3回投げる。1回目,2回目,3回目に出た目の数をそれぞれa,b,cとする。b2−9ac≧０となる(a,b,c)の組は何通りあるか。 【解】b2≧9acより,3≦b≦6 ・b＝3のとき,ac＝1で,1通り ・b＝4のとき,ac＝1で,1通り ・b＝5のとき,ac＝2,3で,3通り ・b＝6のとき,ac＝1〜4で,8通り よって,1＋1＋3＋8＝13通り |
||||||||||||||
| ４ | 慶應義塾志木高校 （Ｒ６年） ★★★ | ７ | 早大本庄高等学院 （Ｒ６年） ★★★ | |||||||||||
 ↑と→の２種類の矢印を左から順に並べてそれに従いＡ地点からマス目状の道を１つずつ進んでいく。(1) ,B地点にたどり着いた。並べ方は何通りか。 【解】計7枚のうち,↑3枚を並べる方法
【解】9枚目までで,PかQに到着 ・Pに到着…↑6枚と→3枚を並べる方法
|
すべてのマス目に次の【ルール】にしたがって自然数を入れる。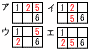 (1) 1と6がすでに入っているとき【解】2と5の入れ方は4パターン 残り3と4の入れ方はア〜エで, 1＋2＋1＋1＝5通り  (2) 1と4と8がすでに入っているとき,【解】2と7の入れ方は4パターン 残り3,5,6の入れ方はア〜エで, 1＋1＋1＋1＝4通り 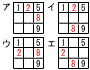 (3) 1と5と9がすでに入っているとき,【解】2と8の入れ方は4パターン 残り3,4,6,7の入れ方はア〜エで, 2＋3＋3＋4＝12通り |
|||||||||||||