 データの活用 |
７ 四分位数・箱ひげ図３ （略解） |
| データの活用 |
７ 四分位数・箱ひげ図３ （略解） |
| １ | 京都府立南陽高校 （Ｒ７年） ★ | ５ | 九州国際高校 （Ｒ６年） ★ | ||||||||
| 次のデータは,数学のテストにおける10人の得点である。 69, 70, 65, 71, 67, 72, 68, 71, x, y (点) テストの平均値が69点,第１四分位数が68点であるとき,xとyの値を求めなさい。ただし,x,yは自然数で,xよリyの方が大きいものとする。 【解】昇順に並べると, 65 67 68 69 70 71 71 72 平均値より,553＋x＋y＝69×10で, x＋y＝137 このとき68≦x＜yだから, x＝68, y＝69 |
 【解】昇順に並べて 9 10 11|12 12 14|15 16 17|17 20 21 ア(最小値)＝9 イ(中央値)＝(14＋15)÷2＝14.5 ウ(第3四分位数)＝17 エ(最大値)＝21 |
||||||||||
| ２ | 桐蔭学園高校 （Ｒ７年） ★ | ６ | 明治大付属明治高校 （Ｒ５年） ★★★ | ||||||||
| 次のデータは10人の生徒の10点満点のテストの得点である。 3, 3, 4, 5, 5,｜6, 8, 8, 8, 10 （点） 転校生が１人入り,このテストを受けたとき,次のような箱ひげ図となった。転校生のテストの得点は[ ]点または[ ]点である。 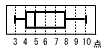 【解】 中央値＝5より, 4点または5点 |
40, 47, 50, 52, 50－x, 50＋x (単位 回) このデータの四分位範囲が8回であるとき, x＝( )である。ただし, xは50以下の自然数とする。 【解】xの値で場合分け Q3(5番目)－Q1(2番目)＝8 ・0＜x≦2のとき, (50＋x)－47＝8より,x＝5(不適) ・2≦x≦3のとき, 52－47≠8 (不適) ・3≦x≦10のとき, 52－(50－x)＝8より, x＝6 (適) |
||||||||||
| ３ | 四天王寺高校 （Ｒ５年） ★★ | ７ | 近畿大附属豊岡高校 （Ｒ５年） ★ | ||||||||
(1) 第１四分位数は(ア )点,中央値は(イ )点,第3四分位数は(ウ )点,四分位範囲は(エ )点です。 【解】 ア Q1(5,6番目の中間)＝(5＋6)÷2＝5.5 イ Q2(10,11番目の中間)＝(9＋10)÷2＝9.5 ウ Q3(15,16番目)＝12 エ Q3－Q1＝12－5.5＝6.5 (2) 欠席生徒が,翌日(オ )点でした。中央値は0.5点増えましたが,第1四分位数と第3四分位数は変わりませんでした｡(オ )にあてはまる整数をすべて書きなさい。 【解】,中央値は10点 オ＝10,11,12のとき, Q2＝10,Q3＝12 (適) オ＝11のとき, Q2＝10,Q3＝12.5 (不適) |
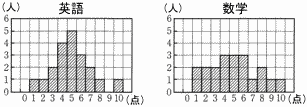 生徒20名の英語と数学の小テストの得点である。(1) 英語の平均値 【解】(1＋2＋6＋16＋25＋18＋14＋8＋10)÷20＝5 (2) 数学の中央値と第３四分位数 【解】 Q2(10,11番目ともに)＝5 Q3(15,16番目の中間)＝(6＋7)÷2＝6.5 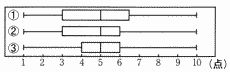 (3) 英語の箱ひげ図【解】 Q1(5,6番目ともに)＝4より, ③ |
||||||||||
| ４ | 愛知県立高校 （Ｒ６年） ★ | ８ | 都立 西 高校 （Ｒ６年） ★ | ||||||||
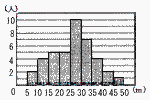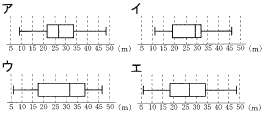 この記録を箱ひげ図で表したとき,最も適当な図を,次のア～エまでの中から選びなさい。 【解】エ 最小値＝5～10 中央値＝25～30 Q1＝15～20 |
 図から読み取れることとして正しく説明しているものを,次のア～エのうちから2つ選び,記号で答えよ。
【解】アエ イ…数学では,20人より多いとは限らない。 ウ…数学には,いるとは限らない。 |
||||||||||