| 6 四分位数・箱ひげ図2 (略解) |
| 6 四分位数・箱ひげ図2 (略解) |
| 1 | 慶応義塾高校 (R7年) ★ | 5 | 國學院大久我山高校 (R7年) ★ | |||||||||||||||||||||||||||
| ある中学校で,9人の生徒に対して100点満点の数学のテストを行った。このテストの得点の最小値は30点,第1四分位数は39点,第2四分位数は64点,第3四分位数は75点,最大値は92点であり,平均値は60点であった。9人のうちの7人の得点が30点,37点,59点,64点,68点,82点,92点であるとき,残り2人の得点は,低い順に[ ]点,
[ ]点である。 ただし,すべての得点は整数値であるものとする。 【解】30 37 x 59 64(Q2) y 68 82 92 残り2人をx,yとすると,平均値より,x+y=108 Q1=(37+x)/2=39より ,x=41点 y=67点 |
次のデータは,16人の生徒の10点満点の計算テストの得点である。
【解】 昇順に並べると, 3, 4, 5, 5, | 5, 6, 6, 6, | 7, 7, 7, 7, | 8, 8, 9, 9 Q1=5 Q2=6.5 Q3=7.5 最小値=3 最大値=9 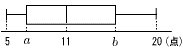 |
|||||||||||||||||||||||||||||
| 2 | 福井県立高校 (R5年) ★ | 6 | 甲南高校 (R7年) ★ | |||||||||||||||||||||||||||
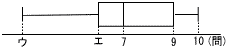 ア〜エと,四分位範囲 ア〜エと,四分位範囲(データ) 3, 4, 6, 6, ア, 8, 8, 9, 9, イ 【解】 中央値=(ア+8)÷2=7より, ア=6 最大値=イ=10 最小値=ウ=3 第1四分位数(3番目)=エ=6 |
次の資料は,生徒9人の10点満点の小テストの結果である。平均値が6点であるとき,aの値と第3四分位数を求めよ。 5,9,6,7,1,9, 3, 6,a 【解】昇順に並べると, 1 3 5 6 6 7 a 9 9 平均値=a+46=6×9より, a=8 Q3=(8+9)/2=8.5 |
|||||||||||||||||||||||||||||
| 3 | 渋谷教育学園幕張高校 (R7年) ★ | 7 | 青山学院高等部 (R7年) ★★★ | |||||||||||||||||||||||||||
| 41以上100未満の異なるすべての素数からなる1組のデータがあります。 (1) 【解】41 43 47 53 59 61 67 71 73 79 83 89 97 ア 第2四分位数Q2を求めなさい。 Q2=67 イ 第3四分位数Q3を求めなさい。 Q3=(79+83)/2=81 (2) このデータから2つの素数を除いて平均値を求めると69となりました。除いた2つの素数を求めなさい。 【解】 2素数の和=(13素数の和)−(11素数の和)=863−759=104 条件を満たすのは, 43と61 |
下図は10人に20点満点のテストを行った結果を箱ひげ図にしたものである。ただし,点数はすべて整数である。 (1) 四分位範囲を求めよ。 【解】13−6=7点 (2) 平均値として考えられる値のうち,最も小さい値(最小値),最も大きい値(最大値)はそれぞれ何点か。 【解】3 a 6 b c d e 13 f 18 (ただし,c+d=20) 平均値=(a+b+e+f+60)/10 最小値=(3+6+10+13+60)/10=9.2点 最大値=(6+10+13+18+60)/10=10.7点 (3) 平均値が整数で,かつ10人全員の点数が異なるとき,10人の点数として考えら れないものを,3点以上18点以下の中ですべて挙げよ。 【解】3 a 6 b 9 11 12 13 f 18 (2)より,平均値=10で,a+b+f=28 (a=4,5 b=7,8 f=14〜17) (a,b,f)=(4,7,17) (4,8,16) (5,7,16) (5,8,15)より, 10点と14点 |
|||||||||||||||||||||||||||||
| 4 | 就実高校 (R6年) ★ | 8 | 長野県立高校 (R6年) ★ | |||||||||||||||||||||||||||
箱ひげ図として正しいものを,下のア〜エから選ぶと[ ]
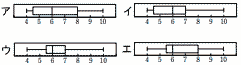 【解】イ 順に並べると,4 4 4 5 6 6 6 7 7 7 9 10 Q1=4.5,Q2=6,Q3=7 |
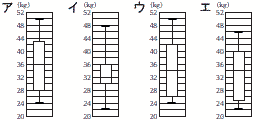 【解】ウ Q1=26 Q2=34 Q3=42 |
|||||||||||||||||||||||||||||