| 俆丂巐暘埵悢丒敔傂偘恾侾丂乮棯夝乯 |
| 俆丂巐暘埵悢丒敔傂偘恾侾丂乮棯夝乯 |
| 侾 | 搚塝擔戝崅峑丂乮俼俈擭乯丂仛 | 俆 | 廹愳崅峑丂乮俼俈擭乯丂仛 | ||||||||||||||||||||||||
| 丂師偺僨乕僞偼9恖偺惗搆偺僥僗僩偺摼揰偱偁傞丅 丂丂丂0, 1, 1, 3, 7, 7, 9, 10, 10 丂巐暘埵斖埻偼[丂丂]揰偱偁傞丅 亂夝亃 Q3亅Q1亖9.5亅1亖8.5揰 |
丂師偺僨乕僞偼10恖偺惗搆偺悢妛偺僥僗僩偺摼揰傪彫偝偄弴偵暲傋偨傕偺偱偁傞丅 丂丂丂丂45, 50, 52 ,56, 56, | 60, 65, 72, 80, 85丂(揰) 丂偙偺僨乕僞偺巐暘埵斖埻傪媮傔側偝偄丅 亂夝亃 Q3亅Q1亖72亅52亖20揰 |
||||||||||||||||||||||||||
| 俀 | 擔戝柧惤崅峑丂乮俼俈擭乯丂仛 | 俇 | 峛撿崅峑丂乮俼俈擭乯丂仛 | ||||||||||||||||||||||||
亂夝亃 Q3(15.5斣栚)亖9 |
丂師偺帒椏偼,惗搆俋恖偺10揰枮揰偺彫僥僗僩偺寢壥偱偁傞丅暯嬒抣偑6揰偱偁傞偲偒,a偺抣偲戞3巐暘埵悢傪媮傔傛丅 丂丂5丆9丆6丆7丆1丆9丆3丆6丆a 亂夝亃暯嬒抣傛傝,a亄46亖6亊9偱,a亖8 徃弴偵暲傋傞偲, 1, 3, 5, 6, 6, 7, 8, 9, 9 丂Q3(7.5斣栚)亖(8亄9)亐2亖8.5 |
||||||||||||||||||||||||||
| 俁 | 戧愳戞擇崅峑丂乮俼俇擭乯丂仛仛 | 俈 | 戝嶃晎棫崅峑丂乮俼俈擭乯丂仛仛 | ||||||||||||||||||||||||
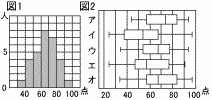 丂壓偺恾2偺傾乣僆偺敔傂偘恾偐傜,恾1偵懳墳偡傞傕偺傪慖傃,婰崋偱摎偊側偝偄丅 丂壓偺恾2偺傾乣僆偺敔傂偘恾偐傜,恾1偵懳墳偡傞傕偺傪慖傃,婰崋偱摎偊側偝偄丅亂夝亃僂 嵟彫抣亖35 嵟戝抣亖95丂,Q1亖55,,Q3亖75 |
亂夝亃徃弴偵暲傋傞偲, 3, 4, 4, 5, 8, 9, 9, 15 Q2(拞墰抣)亖8偩偐傜,Q1亖4偱,Q3亅4亖6傛傝,Q3亖10 丂(9亄x)亐2亖10偲側傟偽傛偄偐傜, x亖11 |
||||||||||||||||||||||||||
| 係 | 偍拑偺悈彈巕戝晬懏崅峑丂乮俼俇擭乯丂仛仛仛 | 俉 | 嶳宍導棫崅峑丂乮俼俈擭乯丂仛 | ||||||||||||||||||||||||
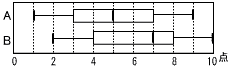 丂敔傂偘恾偼,彫僥僗僩偺寢壥傪昞偟偰偄傞丅 丂敔傂偘恾偼,彫僥僗僩偺寢壥傪昞偟偰偄傞丅(1) 師偺嘆乣嘋偵偮偄偰,惓偟偄傕偺偵偼乑,娫堘偭偰偄傞傕偺偵偼亊,惓岆偑敾抐偱偒側偄傕偺偵偼仮傪婰擖偟側偝偄丅 亂夝亃
(2) A僌儖乕僾偺暯嬒揰傪媮傔側偝偄丅 亂夝亃5揰 A亖{ 1 a b c d e f 9 }偱,a亄b亖6,c亄d亖10,e亄f亖14 暯嬒揰亖(1亄倎亄倐亄乧亄9)亐8亖(30亄1亄9)亐8亖5 (3) B僌儖乕僾偺暯嬒揰偼壗揰埲忋偱偁傞偐摎偊側偝偄丅 亂夝亃6揰埲忋 B亖{ 2 a b c d e f g 10 }偱,a亄b亖8,c亞4,倓亞7,,e亄f亖16 暯嬒揰亞(2亄倎亄倐亄乧亄10)亐9亖(35亄2亄7亄10)亐9亖6 |
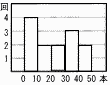 丂塃偺恾偼,偁傞栰媴慖庤偑1擭娫偵懪偭偨儂乕儉儔儞偺杮悢偺13擭暘偺婰榐傪,僸僗僩僌儔儉偵昞俴偨傕偺偱偁傞丅偙偺僸僗僩僌儔儉偐傜,偨偲偊傁,婰榐偑0杮埲忋10杮枹枮偺奒媺偵擖傞擭偼4夞偱偁傞偙偲偑傢偐傞丅 丂塃偺恾偼,偁傞栰媴慖庤偑1擭娫偵懪偭偨儂乕儉儔儞偺杮悢偺13擭暘偺婰榐傪,僸僗僩僌儔儉偵昞俴偨傕偺偱偁傞丅偙偺僸僗僩僌儔儉偐傜,偨偲偊傁,婰榐偑0杮埲忋10杮枹枮偺奒媺偵擖傞擭偼4夞偱偁傞偙偲偑傢偐傞丅丂偙偺僸僗僩僌儔儉傪偮偔傞偺偵傕偲偵偟偨婰榐傪,敔傂偘恾偵昞偟偨傕偺偲俴偰嵟傕揔愗側傕偺傪,師偺傾乣僆偐傜侾偮慖傃,婰崋偱摎偊側偝偄丅 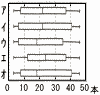 亂夝亃傾 亂夝亃傾Q1(3.5斣栚)亖0乣10 Q2(7斣栚)亖20乣30 Q3(10.5斣栚)亖30乣40 |
||||||||||||||||||||||||||
| 俋 | 搒棫崙棫崅峑丂乮俼俈擭乯丂仛仛仛 | ||||||||||||||||||||||||||
| 丂a傪帺慠悢偲偡傞丅7屄偺悢 a, 2, 2, 5, | 7, 8, 9 偺暯嬒抣偲拞墰抣偑堦抳偡傞偲偒,戞3巐暘埵悢偲側傝摼傞悢傪慡偰媮傔傛丅 亂夝亃暯嬒抣亖(a亄33)/7亖Q2 丒a亝5偺偲偒, (a亄33)/7亖5偱, a亖2(揔)丂偙偺偲偒,Q3亖8 丒5亙a亙7偺偲偒, (a亄33)/7亖a偱, a亖11/2(晄揔) 丒7亝a偺偲偒, (a亄33)/7亖7偱, a亖16(揔)丂偙偺偲偒,Q3亖9丂 丂 |
|||||||||||||||||||||||||||