データの活用 ４　代表値３　（略解）
１ 城西大附属城西高校　（Ｒ７年）　★ ６ 都立 西 高校　（Ｒ５年）　★
　あるクラスの生徒10人が小テストを受けた。得点は次のとおりである。
　　5, 4, 7, a, 3, 7, 9, 4, 4, 8
このとき,中央値が5.5であるときaの値を求めよ。

【解】昇順に並べて, 3, 4, 4, 4, 5, a, 7, 7, 8, 9 となればよい
中央値＝(5＋a)÷2＝5.5より, a＝6
得点(点) 0 5 10 15 20 計
度数(人 2 x 3 y 11 40
　中央値が12.5点であるとき, x,y の値を求めよ。

【解】
下位(0,5,10)と上位(15,20)に等分できる
2＋x＋3＝20, y＋11＝20より
　x＝15　y＝9
２ 鹿屋中央高校　（Ｒ７年）　★ ７ 大阪教育大平野校舎　（Ｒ５年）　★
階級値 度数 積
10 1 10
14 2 28
18 5 90
22 7 154
26 4 104
30 1 30
計 20 416
　表は,A中学校の生徒20人のハンドボール投げの記録を,度数分布表に整理したものです。 この度数分布表から,ハンドボール投げの記録の平均値を求めなさい。

【解】
(階級値)×(度数)の総和＝416より,
　平均値＝416÷20＝20.8m		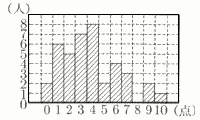 　図は,40人で的あてゲームを行つた得点と人数を表したヒストグラムである。
　このデータについて,以下のものを求めなさい。

(1) 得点の最頻値
【解】
最多は8人で,4点

(2) 40人の得点の平均値
【解】
(1×6＋2×5＋…＋9×2＋10)÷40
　　＝152÷40＝3.8点

(3) 得点の中央値
【解】
20番目は3点で,21番目は4点
(3＋4)÷2＝3.5点
３ 三重高校　（Ｒ７年）　★★★
　aを１けたの自然数とする。5個の数 1, 2, 6, 7 ,a において,平均値と中央値が一致するとき, a＝[　　]である。

【解】平均値＝(a＋16)/5
・a≦2のとき, (a＋16)/5＝2より, a＝−6（不適）
・2＜a＜6のとき, (a＋16)/5＝aより, a＝4（適）
・6≦aのとき, (a＋16)/5＝6より, a＝14（不適）
　
４ 雲雀丘学園高校　（Ｒ７年）　★★★ ８ 桐朋高校　（Ｒ７年）　★★★
　aを整数とする。データ 2, 8, 6, 5, a の中央値と,別のデータ 10, −1, 7, 5, a＋2 の平均値が一致するようなaをすべて求めよ。

【解】別のデータの平均値＝(a＋23)/5
・a≦5のとき, (a＋23)/5＝5より, a＝2（適）
・5＜a＜6のとき, (a＋23)/5＝aより, a＝23/4（不適）
・6≦aのとき, (a＋23)/5＝6より, a＝7（適）
　		 　7個の正の整数 25，48，59，71，13，36，n.がある。これら7個の数の平均値と中央値が等しくなるようなnの値をすべて求めよ。

【解】昇順は, 13,25,36,48,59,71,　平均値＝(n＋252)/7
・a≦36のとき, (n＋252)/7＝36より, n＝0（不適)
・36＜a＜48のとき, (n＋252)/7＝nより, n＝42（適)
・48＜aのとき, (n＋252)/7＝48より, n＝84（適)
５ 都立国立高校　（Ｒ６年）　★★ ９ 都立青山高校　（Ｒ６年）　★
　a,bを1以上6以下の自然数とする。
　4個の数a,b,2,6において,中央値と平均値が一致するa,bの組合せは全部で何通りあるか。

【解】以下の7通り
4数 平・中 a,b
1,2,5,6 3.5 ×2
2,2,6,6 4 ×2
2,3,5,6 4 ×2
2,4,4,6 4 ×1
　次の表は,20人の生徒に5点満点のテストを行ったとき,3点を基準にして,得点から基準を引いた値ごとの人数をまとめたものである。
　このテストの平均点が3.4点のとき,表中のmの値を求めよ。
得点から基準を引いた値(点) -3 -2 -1 0 1 2
人　数　（人） 0 1 m 5 n 4

【解】人数より,m＋n＝10…ア
平均点より,0−2−m＋0＋n＋8＝(3.4−3)×20
　整理すると,−m＋n＝2…イ
(ア−イ)÷2より, m＝4

［TOP］　［問題に戻る］　　★　中　　★★　やや難　　★★★　難