| １ |
和歌山県立高校 （Ｒ５年） ★ |
５ |
筑波大f附属坂戸高校 （Ｒ７年） ★ |
| 通学時間(分) |
度数(人) |
相対度数 |
累積度数(人) |
以上 未満
0〜10 |
24 |
＊ |
＊ |
| 10〜20 |
56 |
＊ |
＊ |
| 20〜30 |
64 |
0.32 |
イ |
| 30〜40 |
40 |
0.20 |
＊ |
| 40〜50 |
16 |
ア |
＊ |
| 計 |
200 |
1.00 |
- |
次の表は,ある学年の生徒の通学時間を調査し,その結果を度数分布表にまとめたものである。表中のア,イにあてはまる数をそれぞれ求めなさい。
【解】
ア 16÷200＝0.08
イ 24＋56＋64＝144 |
51,60,32,75,91,40,62,68,80,30
25,82,96,55,78,66,58,70,88,63 |
次のデータは,あるクラス20人を対象に100点満点のテストを行った結果です。それらを度数分布表にまとめたとき,ア〜ウに当てはまる数を答えなさい。
【解】まず,度数を数えあげる
| 階 級 |
度 数 |
相対度数 |
累積相対度数 |
| 0以上10未満 |
0 |
0.00 |
0.00 |
| 10 〜 20 |
ア 0 |
0.00 |
0.00 |
| 20 〜 30 |
1 |
0.05 |
0.05 |
| 30 〜 40 |
2 |
0.10 |
0.15 |
| 40 〜 50 |
1 |
0.05 |
0.20 |
| 50 〜 60 |
3 |
イ 0.15 |
0.35 |
| 60 〜 70 |
5 |
0.25 |
0.60 |
| 70 〜 80 |
3 |
0.15 |
ウ 0.75 |
| 80 〜 90 |
3 |
0.15 |
0.90 |
| 90 〜100 |
2 |
0.10 |
1.00 |
| 計 |
20 |
1 |
− |
|
| ２ |
近大和歌山高校 （Ｒ７年） ★ |
| 階級（分） |
度数 |
相対度数 |
| 0 〜 10 |
6 |
0.10 |
| 10 〜 20 |
24 |
0.40 |
| 20 〜 30 |
21 |
0.35 |
| 30 〜 40 |
9 |
0.15 |
| 計 |
60 |
1.00 |
右の表は,生徒60人の通学時間について調べた結果を相対度数で表したものです。 通学時間の短い方から数えて40番目の生徒が入っている階級の階級値を求めなさい。
【解】相対度数から度数を求める
40番目は20〜30の階級で, 25分
|
| ３ |
宮城県立高校 （Ｒ７年） ★ |
６ |
函館ラ・サール高校 （Ｒ７年） ★ |
| 秒) |
A 組 |
B 組 |
| 度数(人) |
累積度数(人) |
度数(人) |
累積度数(人) |
以上 未満
140〜160 |
4 |
4 |
3 |
3 |
| 160〜180 |
5 |
9 |
6 |
9 |
| 180〜200 |
7 |
16 |
9 |
18 |
| 200〜220 |
6 |
22 |
10 |
28 |
| 220〜240 |
3 |
25 |
2 |
30 |
| 合計 |
25 |
− |
30 |
− |
ある学年で,クロールで25mを泳いだときの記録をとりました｡下の表は,このときの,A組の生徒25人とB組の生徒30人の記録を,累積度数をふくめて度数分布表に整理したものです。
A組とB組を比べたとき,180秒以上200秒未満の階級の累積相対度数が大きい組と,その累積相対度数を答えなさい。
【解】A組で,0.64
A組＝16÷25＝0.64
B組＝18÷30＝0.6０ |
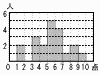 あるクラスの生徒全員に10点満点の小テストを行った。その結果をヒストグラムで表すと図のようになった。
(1) このデータの平均値を求めなさい。
【解】
平均値＝(1.5×2＋3.5×3＋…＋9.5×1)÷20
＝110÷20＝5.5点
(2) 得点の低い方から数えて4番目の得点が入っている階級の相対度数を求めなさい。
【解】4番目は3〜4点の階級で,3人
相対度数＝3÷20＝0.15
|
| ４ |
大阪産大高校 （Ｒ６年） ★ |
７ |
神戸学院大附属高校 （Ｒ６年） ★ |
| 点数(点) |
度数(人) |
| 男子 |
女子 |
| 0以上10未満 |
x |
4 |
| 10 〜 20 |
y |
x |
| 20 〜 30 |
6 |
y |
| 30 〜 40 |
11 |
9 |
| 40 〜 50 |
8 |
7 |
| 計 |
40 |
35 |
右の表は,男子40人と女子35人の50点満点の数学のテストの結果を,度数分布表に整理したものである。 このテストでは満点である50点の生徒はおらず,男女別に各階級の相対度数を求めたところ,10点以上20点未満の階級の相対度数が等しくなりました。x,yの値をそれぞれ求めなさい。
| 【解】 |
 |
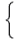x＋y＝15…ア |
|
y |
＝ |
x |
…イ |
|
40 |
35 |
アイを連立させて解くと, x＝7, y＝8 |
| 階級 |
度数 |
相対 |
| 50〜 |
4 |
ア |
| 60〜 |
3 |
|
| 70〜 |
6 |
|
| 80〜 |
2 |
イ |
| 90〜 |
1 |
|
| 計 |
16 |
|
下の数は,あるクラスの生徒16名の数学のテストの得点である。度数分布表のア,イに入る数を,小数第3位を四捨五入して小数第2位まで求めなさい。
56 70 89 67 66 73 62 75 74
53 77 58 74 80 92 56 |
【解】各階級の度数を数える
ア＝4÷16＝0.25
イ＝2÷16≒0.13
|
データの活用