| �R�P�@���ʑ́@�i�����j | ||
| �R�P�@���ʑ́@�i�����j | ||
| �P | ����a�w�����Z�@�i�q�V�N�j�@���� | �S | �c��`�m�u�؍��Z�@�i�q�U�N�j�@������ | |||||||
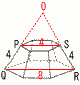 �@��ʂ̐��Z�p�`�̈�ӂ̒�����2�ł���,���ʂ̒����`�̖ʐς�4 �@��ʂ̐��Z�p�`�̈�ӂ̒�����2�ł���,���ʂ̒����`�̖ʐς�4(1) ���Z�p���̑̐ς����߂�B �y���z����(�����`)�̍�����2 ���(���Z�p�`)�� �̐ρ�6 (2) ����AB�̒��������߂�B �y���z��ABC��,AB����(2��3)2�{2(��3)2��2 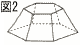 (3) ����MN�̒��������߂�B (3) ����MN�̒��������߂�B �y���z���ʐ}�ōl���� ��ACD��,MN�� (4) �l�ʑ�BCMN�̑̐ς����߂�B �y���z��PMN�� (�O�p����C-PMN)�{(�O�p����B-PMN) �@��( |
�@���ʑ̂̊e���_�ɏW�܂�e�ӂ�3��������_�̂���,���_�ɋ߂����̓_�����ׂĒʂ镽�ʂŗ��̂��,���_���܂ފp������菜���ĐV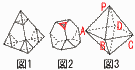 �������̂���鑀����m����1�n�Ƃ���B�Ⴆ���}1�̐��l�ʑ̂Ɂm����1�n�������,�}2�̂悤�ȗ��̂��ł���B �������̂���鑀����m����1�n�Ƃ���B�Ⴆ���}1�̐��l�ʑ̂Ɂm����1�n�������,�}2�̂悤�ȗ��̂��ł���B(1) �}3�̂悤��1�ӂ̒�����9�̐����ʑ̂Ɂm����1�n�������Ƃ��ɂł��闧�̂̑̐�V1�����߂�B �y���z ���l�p��P-ABCD= ���鏬�l�p�����A�~ �̐�V1���A�~2�|�C�~6��243 (2) (1)�łł������̂ɑ���,����Ɂm����1�n�������Ƃ��ɂł��闧�̂̑̐�V2�����߂�B �y���z�}2(�ؒ����ʑ�)��,�����`6,���Z�p�`8,���_14 ���鏬�O�p���� �̐�V2��V1�| |
|||||||||
| �Q | �_�ސ쌧�����Z�@�i�q�V�N�j�@���� | �T | �}�g�啍����ꍂ�Z�@�i�q�T�N�j�@������ | |||||||
 �@���̎l�p���ɂ�����,3�_I,J,K������łł��� �O�p�`�̖ʐ� [�@�@]cm2�ł���B �@���̎l�p���ɂ�����,3�_I,J,K������łł��� �O�p�`�̖ʐ� [�@�@]cm2�ł���B�y���z��IML�߁�IMJ�߁�JML ��IJL��1��6 �@�ʐρ� ��IJK����IJL�~ �@ |
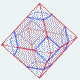 (1) �ʂ����10cm�̐����`��,���ʂ����10cm�̐��O�p�`�ł��鐳�l�p�����̑̐� (1) �ʂ����10cm�̐����`��,���ʂ����10cm�̐��O�p�`�ł��鐳�l�p�����̑̐��y���z �̐ρ� (2) ���10cm�̐����`6�ƈ��10cm�̐��Z�p�`8�ō��ꂽ���ʑ�(�ؒ����ʑ��Ƃ���)�̑̐� �y���z���30cm�̐����ʑ́|(1)�~6
|
|||||||||
| �R | ���썂�Z�@�i�q�T�N�j�@������ | �U | ����c�卂���w�@�@�i�q�T�N�j�@������ | |||||||
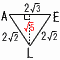 (1) ���ׂĂ̕ӂ̒�����2�̐��Z�p��ABCDEF-GHIJKL������܂��B (1) ���ׂĂ̕ӂ̒�����2�̐��Z�p��ABCDEF-GHIJKL������܂��B(�) ��AEL�̖ʐ�(�E�}) �y���z�ӎO�p�` 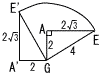 ��AEL�� ��AEL��(�) �l�ʑ�AEIL�̑̐� �y���z(�O�p��A-MLI)�|(�O�p��E-MLI) �̐ρ�2( (2) (�) �菇�@�Œʉ߂���ʐ� 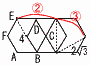 �y���z��AGE�{��`GEE'(�E��}) �y���z��AGE�{��`GEE'(�E��})�ʐρ� (�) �菇�@�`�C�ŋȐ��̒����̘a �y���z �菇�A��8���~ E���`���Ȑ�PE����22�{(��3)2�� 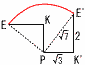 �@�菇�C��2 �@�菇�C��2�����̘a��(2�{
|
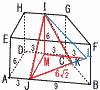
(1) ���ʑ�P(���l�p�����Ƃ���)�̕\�ʐ� �y���z�����`2�{���O�p�`8�� 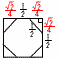 �\�ʐρ�12�~2�{ �\�ʐρ�12�~2�{(2) �f�ʂ̐}�`�̖ʐ� �y���z1�� �f�ʐρ�( (3) ���̒��������߂�B �y���z�l�p�`DGEA ���̒����� 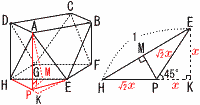 (4) h2�̒l�����߂�B �y���zh��AP�Ƃ��� ��EHK��, �@(��2x�{x)2�{x2��12 �@x2��1/(4�{2 ��APM��,h2��AM2�|PM2��AM2�|(PE2�|EM2) �@��( |
|||||||||