 図形 |
３１ 多面体 | 月 日（ ） |
| 図形 |
３１ 多面体 | 月 日（ ） |
| １ | 西大和学園高校 （Ｒ７年） ★★ | ４ | 慶應義塾志木高校 （Ｒ６年） ★★★ |
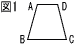 底面の正六角形の一辺の長さが2であり,側面の長方形の面積が4 である正六角柱について考える。図のように頂点A,B,C,Dをとり,AB,CDの中点をそれぞれM,Nとする。(1) 正六角柱の体積を求めよ。 (2) 線分ABの長さを求めよ。 (3) 線分MNの長さを求めよ。 (4) 四面体BCMNの体積を求めよ。 |
多面体の各頂点に集まる各辺を3等分する点のうち,頂点に近い方の点をすべて通る平面で立体を切り,頂点を含む角錐を取り除いて新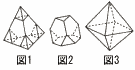 しい立体を作る操作を［操作1］とする。例えば図１の正四面体に［操作1］をすると,図2のような立体ができる。(1) 図3のような１辺の長さが9の正八面体に［操作1］をしたときにできる立体の体積V1を求めよ。 (2) (1)でできた立体に対して,さらに［操作1］をしたときにできる立体の体積V2を求めよ。 |
||
| ２ | 神奈川県立高校 （Ｒ７年） ★★ | ５ | 筑波大附属駒場高校 （Ｒ５年） ★★★ |
 右の図は,AB//DC,∠BＡD＝90°,AB＝12cm, AD＝CD＝6cmの台形ABCDを底面とし,AE＝BF＝CG＝DH＝6cmを高さとする四角柱である。
また,点Iは辺GHの中点であり,点Jは辺AB上の点で,AJ:JB＝1:3である。 さらに,点Kは辺BC上の点で,BK:KC＝3:1である。この四角柱において,3点I,J,Kを結んでできる 三角形の面積 [ ]cm2である。 |
(1) 底面が一辺10cmの正方形で,側面が一辺10cmの正三角形である正四角すいの体積を求めなさい。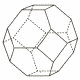 (2) 右の図のような,一辺10cmの正方形6個と一辺10cmの正六角形8個で作られた多面体の体積を求めなさい。 |
||
| ３ | 洛南高校 （Ｒ５年） ★★★ | ６ | 早稲田大高等学院 （Ｒ５年） ★★★ |
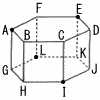 (1) 図のように,すべての辺の長さが2の正六角柱ABCDEF-GHIJKLがあります。(ｱ) △AELの面積を求めなさい。 (ｲ) 四面体AEILの体積を求めなさい。 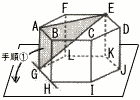 (2) 次に,(1)の正六角柱を,図のように面GHIJKLが下になるように,台の上に置きます。 この状態からすべらせることなく,以下の手順で台の上を転がします。 手順① 辺GHを軸として面AGHBが台につくまで転がす。 手順② 辺BHを軸として面BHICが台につくまで転がす。 手順③ 辺CIを軸として面CIJDが台につくまで転がす。 手順④ 辺IJを軸として面GHIJKLが台につくまで転がす。 (ｱ) 手順①で△AEGが通過する部分の面積を求めなさい。 (ｲ) 手順①から④で点Eが描く曲線の長さの和を求めなさい。 |
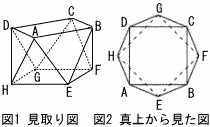 図1,図2のような多面体Pについて考える。多面体Pの上面の四角形ABCD,底面の四角形 EFGHはいずれも 1辺の長さが1の正方形であり,四角形ABCDを含む平面と四角形EFGHを含む平面は平行である。また,側面の三角形はすべて正三角形である。 (1) 多面体Pの表面積を求めよ。 (2) 辺AE,EB,BFの中点をそれぞれL,M,Nとする。3点L,M,Nを通る平面で多面体Pを切ったときにできる断面の図形の面積を求めよ。 (3) 3点D,E,Gを通る平面で多面体Pを切ったときにできる断面の図形の周の長さを求めよ。 (4) 四角形ABCDを含む平面と四角形EFGHを含む平面との距離をhとするとき,h2の値を求めよ。 |
||
